题目内容
给定一列按规律排列的数:1,
,
,
,…,则这列数的第9个数是( )
| 4 |
| 3 |
| 3 |
| 2 |
| 8 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:规律型:数字的变化类
专题:
分析:把数列1,
,
,
,…,变为
,
,
,
,…,可知分子是从2开始连续的偶数,分母是从2开始连续的自然数,由此规律解决问题即可.
| 4 |
| 3 |
| 3 |
| 2 |
| 8 |
| 5 |
| 2 |
| 2 |
| 4 |
| 3 |
| 6 |
| 4 |
| 8 |
| 5 |
解答:解:把数列1,
,
,
,…,变为
,
,
,
,…,
则第n个数为
,
所以这列数的第9个数是
=
.
故选:B.
| 4 |
| 3 |
| 3 |
| 2 |
| 8 |
| 5 |
| 2 |
| 2 |
| 4 |
| 3 |
| 6 |
| 4 |
| 8 |
| 5 |
则第n个数为
| 2n |
| n+1 |
所以这列数的第9个数是
| 18 |
| 10 |
| 9 |
| 5 |
故选:B.
点评:此题考查数字的排列规律,找出数字之间的联系,找出规律,解决问题.

练习册系列答案
相关题目
我区面积1420平方千米,请你估计,它的千万分之一大约相当于( )
| A、一本课本的面积 | B、一块黑板的面积 | C、一个操场的面积 | D、一套住宅的面积 |
化简a-2a=( )
| A、-2 | B、-a | C、a | D、3a |
观察下列数表:
1 2 3 4…第一行
2 3 4 5…第二行
3 4 5 6…第三行
4 5 6 7…第四行
根据数表所反映的规律,第n行第n列交叉点上的数应为( )
1 2 3 4…第一行
2 3 4 5…第二行
3 4 5 6…第三行
4 5 6 7…第四行
根据数表所反映的规律,第n行第n列交叉点上的数应为( )
| A、2n-1 | B、2n+1 | C、n2-1 | D、n2 |
已知an=
(n=1,2,3,…),我们又定义b1=2(1-a1)=
,b2=2(1-a1)(1-a2)=
,b3=2(1-a1)(1-a2)(1-a3)=
,…,根据你观察的规律可推测出bn=( )
| 1 |
| (n+1)2 |
| 3 |
| 2 |
| 4 |
| 3 |
| 5 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列图形都是由同样大小的正方形按一定规律组成的,其中,第1个图形中一共有1个正方形,第2个图形中共有5个正方形,第3个图形中共有14个正方形,…,按照此规律第5个图形中正方形的个数为( )


| A、30 | B、46 | C、55 | D、60 |
如图①是一块瓷砖的图案,用这种瓷砖铺设地面,如果铺设成如图②的图案,其中完整的圆一共有5个,如果铺设成如图③的图案,其中完整的圆一共有13个,如果铺设成如图④的图案,其中完整的圆一共有25个,以此规律下去,第10个图中,完整的圆一共有( )
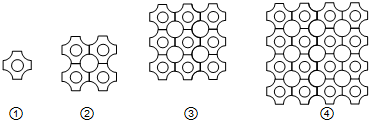

| A、100个 | B、101个 | C、181个 | D、221个 |
下列式子中( )是方程.
| A、2+3-X | B、3+X>5 | C、3-y=1 | D、以上都不是 |
 图①是由白色纸板拼成的立体图形,将它的两个面的外表面涂上颜色,如图②.则下列图形中,是图②的表面展开图的是( )
图①是由白色纸板拼成的立体图形,将它的两个面的外表面涂上颜色,如图②.则下列图形中,是图②的表面展开图的是( )


