题目内容
如图是一串有趣的图案按一定的规律排列，请仔细观察，按此规律第2014个图案是（ ）
A、 | B、 | C、 | D、 |
考点：规律型：图形的变化类
专题：
分析：观察不难发现，每4个图案为一个循环组依次循环，用2014÷4，根据能够整除可知第2014个图案与第2个图案相同．
解答：解：观察图案可知，每4个图案为一个循环组依次循环，
∵2012÷4=503…2，
∴第2014个图案为第504循环组的第二个图案，与第2个图案相同．
故选B．
∵2012÷4=503…2，
∴第2014个图案为第504循环组的第二个图案，与第2个图案相同．
故选B．
点评：本题是对图形变化规律的考查，比较简单，观察出每4个图案为一个循环组依次循环是解题的关键．
练习册系列答案
快乐5加2金卷系列答案
相关题目
下列各式：①1
x；②2•3；③20%x；④a-b÷c；⑤
；⑥x-5；其中，不符合代数式书写要求的有（ ）
| 1 |
| 3 |
| m2n2 |
| 3 |
| A、5个 | B、4个 | C、3个 | D、2个 |
已知x-y=3，那么代数式3（x-y）2-2（x-y）-2（x-y）2+x-y的值是（ ）
| A、3 | B、27 | C、6 | D、9 |
已知an=
（n=1，2，3，…），我们又定义b1=2（1-a1）=
，b2=2（1-a1）（1-a2）=
，b3=2（1-a1）（1-a2）（1-a3）=
，…，根据你观察的规律可推测出bn=（ ）
| 1 |
| (n+1)2 |
| 3 |
| 2 |
| 4 |
| 3 |
| 5 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，下列图形都是由面积为1的正方形按一定的规律组成，其中，第（1）个图形中面积为1的正方形有2个，第（2）个图形中面积为1的正方形有5个，第（3）个图形中面积为1的正方形有9个，…，按此规律．则第（6）个图形中面积为1的正方形的个数为（ ）
| A、20 | B、27 | C、35 | D、40 |
如图①是一块瓷砖的图案，用这种瓷砖铺设地面，如果铺设成如图②的图案，其中完整的圆一共有5个，如果铺设成如图③的图案，其中完整的圆一共有13个，如果铺设成如图④的图案，其中完整的圆一共有25个，以此规律下去，第10个图中，完整的圆一共有（ ）
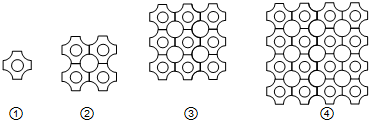
| A、100个 | B、101个 | C、181个 | D、221个 |
下列图①中有3个小黑圆点，图②中有8个小黑圆点，图③中有15个小黑圆点，按照此规律，第10个图形中小黑圆点的个数为（ ）
| A、39 | B、63 | C、99 | D、120 |
若关于x的方程4x-m+2=3x-l的解为正数，则m的取值范围是（ ）
| A、m＞-1 | B、m＞-3 | C、m＞3 | D、m＜3 |
如图，把左边的图形折叠起来，它会变为右面的哪幅立体图形（ ）A、 | B、 | C、 | D、 |