��Ŀ����
����Ŀ��P�ǡ�O��һ�㣬����P����O������һ����AB�����ǰ�PAPB��ֵ��Ϊ��P���ڡ�O������ֵ��
��1����O�İ뾶Ϊ6��OP=4��
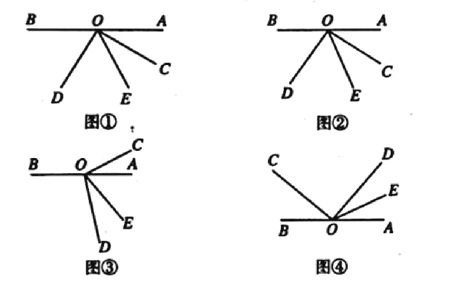
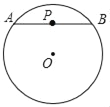
����ͼ1������PǡΪ��AB���е㣬���P���ڡ�O������ֵ��Ϊ_____��
���жϵ���AB��λ�øı�ʱ����P���ڡ�O������ֵ���Ƿ�Ϊ��ֵ�����Ƕ�ֵ��֤����Ľ��ۣ������Ƕ�ֵ�����P���ڡ�0������ֵ����ȡֵ��Χ��
��2������O�İ뾶Ϊr��OP=d����ο���1����˼·���ú�r��d��ʽ�ӱ�ʾ��P���ڡ�O������ֵ��������ֵ����ȡֵ��Χ_____��
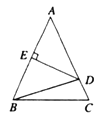
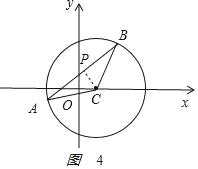
��3����ƽ��ֱ������ϵxOy�У�C��1��0������C�İ뾶Ϊ3������ֱ��y=![]() x+b�ϴ��ڵ�P��ʹ�õ�P���ڡ�C������ֵ��Ϊ6����ֱ��д��b��ȡֵ��Χ_____��
x+b�ϴ��ڵ�P��ʹ�õ�P���ڡ�C������ֵ��Ϊ6����ֱ��д��b��ȡֵ��Χ_____��
���𰸡���1����20���ڵ���AB��λ�øı�ʱ����P���ڡ�O������ֵ��Ϊ��ֵ��֤������������2����P���ڡ�O������ֵ��Ϊr2��d2����3����3![]() ��b��
��b��![]() .
.
������������⡿��1������ͼ1��ʾ������OA��OB��OP���ɵ��������ε����ߺ�һ�����ʵõ���PBOΪֱ�������Σ�Ȼ�����ݹ��ɶ��������PB�ij���Ȼ��������ֵ�Ķ�����⼴�ɣ�
�ڹ���P����O����A��B����OP������AA�䡢BB������֤����APA���ס�B��PB���������������ε����ʵõ�PAPB=PA��PB���Ӷ��ó����ۣ�
��2������OP������P��AB��OP����ԲO��A��B���㣮�ɵ������������ߺ�һ�����ʿ�֪AP=PB��Ȼ����Rt��APO�У����ݹ��ɶ�����֪AP2=OA2-OP2��Ȼ��d��r����ɵõ�����Ĵ𰸣�
��3������C��CP��AB�������OP�Ľ���ʽ��Ȼ����ֱ��AB��OP�Ľ���ʽ���õ���P�����꣬Ȼ��������Բ����ֵΪ6���뾶Ϊ4�����d��ֵ���ٽ�������ľ��빫ʽ�ɵõ�����b�ķ��̣��Ӷ������b�ļ�ֵ���ݴ˼���ȷ����b��ȡֵ��Χ��
����⡿��1������ͼ1��ʾ������OA��OB��OP��
��OA=OB��PΪAB���е㣬
��OP��AB��
������PBO�У��ɹ��ɶ����ã�PB=![]() =2
=2![]() ��
��
��PA=PB=2![]() ��
��
���O������ֵ��=2![]() ��2
��2![]() =20��
=20��
�ʴ�Ϊ��20��
�ڵ���AB��λ�øı�ʱ����P���ڡ�O������ֵ��Ϊ��ֵ��֤�����£�
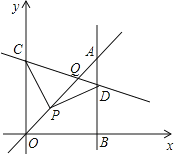
��ͼ��ABΪ��O�й���P������һ���ң��Ҳ���OP��ֱ������P����O����A��B����OP������AA�䡢BB�䣬
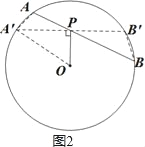
���ڡ�O�У���AA��P=��B��BP����APA��=��BPB�䣬
���APA���ס�B��PB��
��![]() ��
��
��PAPB=PA��PB��=20��
�൱��AB��λ�øı�ʱ����P���ڡ�O������ֵ��Ϊ��ֵ��
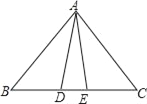
��2����ͼ3��ʾ������OP������P��AB��OP����ԲO��A��B������
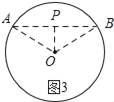
��AO=OB��PO��AB��
��AP=PB��
���P���ڡ�O������ֵ��=APPB=PA2��
��Rt��APO��AP2=OA2��OP2=r2��d2��
����ڡ�O������ֵ��=r2��d2��
�ʴ�Ϊ����P���ڡ�O������ֵ��Ϊr2��d2��
��3����ͼ4
 ��
��
��CP��AB��AB�Ľ���ʽΪy=![]() x+b��
x+b��
��ֱ��CP�Ľ���ʽΪy=��![]() x+
x+![]() ��
��
����AB��CP����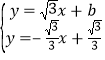 ��
��
���P����������![]() ��
��![]() b��
b��![]() +
+![]() b����
b����
�ߵ�P���ڡ�C������ֵ��Ϊ6��
��r2��d2=6��
��d2=3��������![]() ��
��![]() b��2+��
b��2+��![]() +
+![]() b��2=3��
b��2=3��
�����ã�b2+2![]() b��9=0��
b��9=0��
���b=��3![]() ��b=
��b=![]() ��
��
��b��ȡֵ��Χ�ǩ�3![]() ��b��
��b��![]() ��
��
�ʴ�Ϊ����3![]() ��b��
��b��![]() .
.

����Ŀ��ijѧУ��Ϊ���꼶ѧ������![]() ��6��ѡ�Σ�ѡȡ������ѧ������������ϲ����һ��ѡ�ε��飬�����������Ƴ�����ͼ��ʾ��ͳ��ͼ��������������
��6��ѡ�Σ�ѡȡ������ѧ������������ϲ����һ��ѡ�ε��飬�����������Ƴ�����ͼ��ʾ��ͳ��ͼ��������������
ѡ�� |
|
|
|
|
|
|
���� | 40 | 60 | 100 |
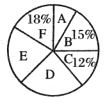
����˵������ȷ���ǣ� ��
A.��α������ѧ������Ϊ400��B.![]() ��Ӧ���ε�Բ�Ľ�Ϊ
��Ӧ���ε�Բ�Ľ�Ϊ![]()
C.ϲ��ѡ��![]() ������Ϊ72��D.ϲ��ѡ��
������Ϊ72��D.ϲ��ѡ��![]() ����������
����������