题目内容
如图,已知Rt△ABC,∠ACB=90°,点O为斜边AB上一点,以点O为圆心、OA为半径的圆与BC相切于点D, 与AB相交于点E,与AC相交于点F,连接OD.
与AB相交于点E,与AC相交于点F,连接OD.
(1)求证:AD平分∠BAC;
(2)若∠BAD=22.5°,⊙O的半径为4,求阴影部分的面积.(结果保留π)
 (1)证明:∵⊙O与BC相切于点D,
(1)证明:∵⊙O与BC相切于点D,∴OD⊥BC,
∴∠ODB=90°(1分)
∵∠ACB=90°,
∴∠ODB=∠ACB(2分)
∴OD∥AC(3分)
∴∠1=∠3(4分)
∵OD=OA,
∴∠1=∠2(5分)
∴∠2=∠3,即AD平分∠BAC(6分)
(2)解:∵∠BAD=22.5°,
∴∠EOD=45°(7分)
∴
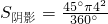 (8分)
(8分)分析:(1)利用切线BC的性质求得∠ODB=90°,再根据已知条件∠ACB=90°,来证明OD∥AC;然后由两直线平行内错角相等知∠1=∠3;最后由等腰三角形AOD的两个底角∠1=∠2及等量代换证明AD平分∠BAC;
(2)由圆周角定理求得∠EOD=2∠BAD=45°;然后利用扇形面积公式=
 来求阴影部分的面积.
来求阴影部分的面积.点评:本题考查了切线的性质、圆周角定理及扇形的面积公式.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
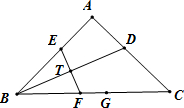 22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.
22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.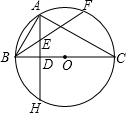 E,交⊙O于点F,且AE=BE.
E,交⊙O于点F,且AE=BE.
 5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF.
5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF.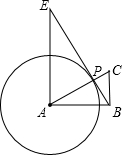 如图,已知Rt△ABC中,∠CAB=30°,BC=5.过点A做AE⊥AB,且AE=15,连接BE交AC于点P.
如图,已知Rt△ABC中,∠CAB=30°,BC=5.过点A做AE⊥AB,且AE=15,连接BE交AC于点P.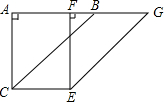 如图,已知Rt△ABC中∠A=90°,AB=3,AC=4.将其沿边AB向右平移2个单位得到△FGE,则四边形ACEG的面积为
如图,已知Rt△ABC中∠A=90°,AB=3,AC=4.将其沿边AB向右平移2个单位得到△FGE,则四边形ACEG的面积为