题目内容
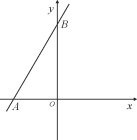
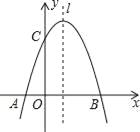
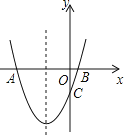
【题目】如图,抛物线y=x2+2x+k+1与x轴交与A、B两点,与y轴交与点C(0,-3).
(1)求抛物线的对称轴及k的值;
(2)求抛物线的对称轴上存在一点P,使得PA+PC的值最小,求此时点P的坐标;
(3)点M是抛物线上的一动点,且在第三象限.
①当M点运动到何处时,△AMB的面积最大?求出△AMB的最大面积及此时点M的坐标.
②当M点运动到何处时,四边形AMCB的面积最大?求出四边形AMCB的最大面积及此时点M的坐标.
【答案】(1)y=(x+1)2-4,直线x=-1(2)(-1,-2)(3)当点M的坐标为(-![]() ,-
,-![]() )时,四边形AMCB的面积最大,最大值为
)时,四边形AMCB的面积最大,最大值为![]()
【解析】
(1)由抛物线y=x2+2x+k+1与y轴交于点C(0,-3),即可将点C的坐标代入函数解析式,解方程即可求得k的值,由抛物线y=x2+2x+k+1即可求得抛物线的对称轴为:x=-1;
(2)连接AC交抛物线的对称轴于点P,则PA+PC的值最小,求得A与C的坐标,设直线AC的解析式为y=kx+b,利用待定系数法即可求得直线AC的解析式,则可求得此时点P的坐标;
(3)①设点M的坐标为:(x,(x+1)2-4),即可得S△AMB=![]() ×4×|(x+1)2-4|,由二次函数的最值问题,即可求得△AMB的最大面积及此时点M的坐标;
×4×|(x+1)2-4|,由二次函数的最值问题,即可求得△AMB的最大面积及此时点M的坐标;
②设点M的坐标为:(x,(x+1)2-4),然后过点M作MD⊥AB于D,由S四边形ABCM=S△OBC+S△ADM+S梯形OCMD,根据二次函数的最值问题的求解方法,即可求得四边形AMCB的最大面积及此时点M的坐标.
(1)∵抛物线y=x2+2x+k+1与y轴交于点C(0,-3),
∴-3=1+k,
∴k=-4,
∴抛物线的解析式为:y=(x+1)2-4,
∴抛物线的对称轴为:直线x=-1;
(2)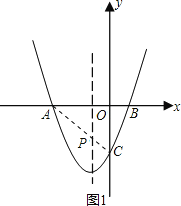
如图1,连接AC交抛物线的对称轴于点P,则PA+PC的值最小,
当y=0时,(x+1)2-4=0,
解得:x=-3或x=1,
∵A在B的左侧,
∴A(-3,0),B(1,0),
设直线AC的解析式为:y=kx+b,则
![]() ,
,
解得![]() ,
,
∴直线AC的解析式为:y=-x-3,
当x=-1时,y=-(-1)-3=-2,
∴点P的坐标为:(-1,-2);
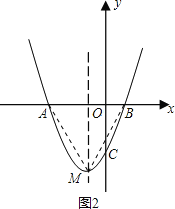
(3)如图2,点M是抛物线上的一动点,且在第三象限,
∴-3<x<0;
①设点M的坐标为:(x,(x+1)2-4),
∵AB=1-(-3)=4,
∴S△AMB=![]() ×4×|(x+1)2-4|=2|(x+1)2-4|,
×4×|(x+1)2-4|=2|(x+1)2-4|,
∵点M在第三象限,
∴S△AMB=8-2(x+1)2,
∴当x=-1时,即点M的坐标为(-1,-4)时,△AMB的面积最大,最大值为8;
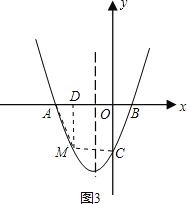
②设点M的坐标为:(x,(x+1)2-4),
如图3,过点M作MD⊥AB于D,则
S四边形ABCM=S△OBC+S△ADM+S梯形OCMD
=![]() ×3×1+
×3×1+![]() ×(3+x)×[4-(x+1)2]+
×(3+x)×[4-(x+1)2]+![]() ×(-x)×[3+4-(x+1)2]
×(-x)×[3+4-(x+1)2]
=-![]() (x2+3x-4)
(x2+3x-4)
=-![]() (x+
(x+![]() )2+
)2+![]() ,
,
∴当x=-![]() 时,y=(-
时,y=(-![]() +1)2-4=-
+1)2-4=-![]() ,
,
即当点M的坐标为(-![]() ,-
,-![]() )时,四边形AMCB的面积最大,最大值为
)时,四边形AMCB的面积最大,最大值为![]() .
.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案