题目内容
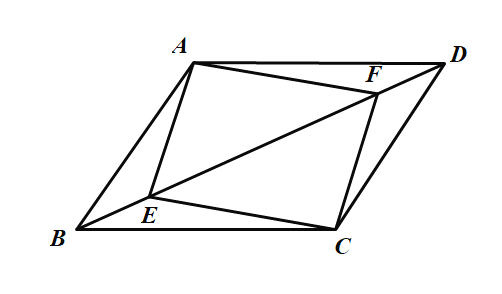
【题目】如图,已知在平行四边形![]() 中,
中,![]() 是对角线
是对角线![]() 上的两点,则以下条件不能判断四边形
上的两点,则以下条件不能判断四边形![]() 是平行四边形的是( )
是平行四边形的是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】
连接AC与BD相交于O,根据平行四边形的对角线互相平分可得OA=OC,OB=OD,再根据对角线互相平分的四边形是平行四边形,只要证明得到OE=OF即可,然后根据各选项的条件分析判断即可得解.
解:如图,连接AC与BD相交于O,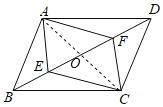
在ABCD中,OA=OC,OB=OD,
要使四边形AECF为平行四边形,只需证明得到OE=OF即可;
A、AF=EF无法证明得到OE=OF,故本选项正确.
B、∠BAE=∠DCF能够利用“角角边”证明△ABE和△CDF全等,从而得到DF=BE,则OB-BE=OD-DF,即OE=OF,故本选项错误;
C、若AF⊥CF,CE⊥AE,由直角三角形的性质可得OE=![]() AC=OF,故本选项错误;
AC=OF,故本选项错误;
D、若BE=DF,则OB-BE=OD-DF,即OE=OF,故本选项错误;
故选:A.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目