[题目]在平面直角坐标系中表示下面各点: A(0.3) B(1.-3) C(3.-5) D(-3.-5) E(3.5).连接CE.CD.(1)A点到原点的距离是个单位长度;B点到直线CD的距离是个单位长度;(2)将点C向x轴的负方向平移6个单位.它与点重合;(3)直线CE与y轴的位置关系是 ;直线CE与x轴的位置关系是 . 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】在平面直角坐标系中表示下面各点：

A（0，3） B（1，-3） C（3，-5） D（-3，-5） E（3，5）.连接CE，CD.

(1)A点到原点的距离是___个单位长度;B点到直线CD的距离是____个单位长度;

(2)将点C向x轴的负方向平移6个单位，它与点_______重合;

(3)直线CE与y轴的位置关系是_______;直线CE与x轴的位置关系是_______.

【答案】（1）3，2;（2） D;（3）平行;垂直.

【解析】

（1）利用点的坐标的意义求解．（2）将点C向x轴的负方向平移6个单位得到对应点的坐标为（-3，5），于是可判断它与点D重合．（3）利用点C和点E的横坐标相同可判断直线CE与坐标轴的关系；

解：作图如下：

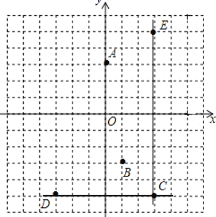
（1）A点到原点的距离是3，B点到直线CD的距离是2．
（2）将点C向x轴的负方向平移6个单位，它与点D重合．
（3）直线CE与y轴平行，与x轴垂直；

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

【题目】图a是一个长为2m，宽为2n的长方形，沿图a中虚线用剪刀把它均分成四块小长方形，然后按图b的形状拼成一个正方形．
（1）请用两种不同的方法求图b中阴影部分的面积：
方法1： ____ （只列式，不化简）
方法2： ______ （只列式，不化简）
（2）观察图b，写出代数式（m+n）2，（m-n）2，mn之间的等量关系： ______ ；
（3）根据（2）题中的等量关系，解决如下问题：若a+b=7，ab=5，

则（a-b）2= ______ ．

【题目】如图，小河边有两个村庄A、B，要在河边建一自来水厂向A村与B村供水。

（1）若要使水厂到A、B村的距离相等，则应选择在哪建厂？　

（2）若要使水厂到A、B村的水管最省料，应建在什么地方？

【题目】一次演讲比赛中，评委将从演讲内容、演讲能力、演讲效果三方面为选手打分，各项成绩均按百分制，进入决赛的两名选手的单项成绩如下表所示：

选手	演讲内容	演讲能力	演讲效果
甲	85	95	95
乙	95	85	95

（1）如果认为这三方面的成绩同等重要，从他们的成绩看，谁能胜出？

（2）如果按演讲内容占50%，演讲能力占40%，演讲效果占10%的比例计算甲、乙的平均成绩，那么谁将胜出？

【题目】如图，AB=12cm，点C是线段AB上的一点，BC=2AC．动点P从点A出发，以3cm/s的速度向右运动，到达点B后立即返回，以3cm/s的速度向左运动；动点Q从点C出发，以1cm/s的速度向右运动．设它们同时出发，运动时间为ts．当点P与点Q第二次重合时，P，Q两点停止运动．

（1）AC= cm，BC= cm；

（2）当t为何值时，AP=PQ；

（3）当t为何值时，P与Q第一次相遇；

（4）当t为何值时，PQ=1cm．

【题目】如图（1），是两个全等的直角三角形（直角边分别为a，b，斜边为c）．

（1）用这样的两个三角形构造成如图（2）的图形（B，E，C三点在一条直线上），利用这个图形，求证：a2+b2=c2

（2）当a=1，b=2时，将其中一个直角三角形放入平面直角坐标系中（如图（3）），使直角顶点与原点重合，两直角边a，b分别与x轴、y轴重合．

请在坐标轴上找一点C，使△ABC为等腰三角形．

写出一个满足条件的在x轴上的点的坐标：　　；

写出一个满足条件的在y轴上的点的坐标：　　，这样的点有　　个．

【题目】某科技有限公司准备购进A和B两种机器人来搬运化工材料，已知购进A种机器人2个和B种机器人3个共需16万元，购进A种机器人3个和B种机器人2个共需14万元，请解答下列问题：

（1）求A、B两种机器人每个的进价；

（2）已知该公司购买B种机器人的个数比购买A种机器人的个数的2倍多4个，如果需要购买A、B两种机器人的总个数不少于28个，且该公司购买的A、B两种机器人的总费用不超过106万元，那么该公司有哪几种购买方案？

【题目】一组对边平行，另一组对边相等且不平行的四边形叫做等腰梯形．
（1）类比研究
我们在学完平行四边形后，知道可以从对称性、边、角和对角线四个角度对四边形进行研究，完成表．

四边形	对称性	边	角	对角线
平行四边形	．	两组对边分别平行，两组对边分别相等．	两组对角分别相等．	对角线互相平分．
等腰梯形	轴对称图形，过平行的一组对边中点的直线是它的对称轴．	一组对边平行，另一组对边相等．	．	．

（2）演绎论证
证明等腰梯形有关角和对角线的性质．
已知：在等腰梯形ABCD中，AD∥BC，AB=DC，AC、BD是对角线．
求证：
证明：
揭示关系
我们可以用图来揭示三角形和一些特殊三角形之间的关系．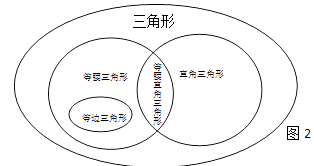

（3）请用类似的方法揭示四边形、对角线相等的四边形、平行四边形、矩形以及等腰梯形之间的关系．

试题分类