题目内容
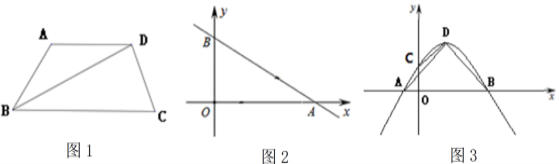
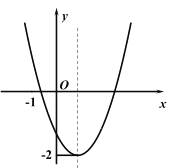
【题目】已知二次函数![]() 的图象如图所示,并且关于
的图象如图所示,并且关于![]() 的一元二次方:
的一元二次方:![]() 有两个不相等的实数根,下列结论:①
有两个不相等的实数根,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确的有__________.
,其中正确的有__________.
【答案】③
【解析】
① 利用![]() 可以用来判定二次函数与x轴交点个数,即可得出答案;② 根据图中当
可以用来判定二次函数与x轴交点个数,即可得出答案;② 根据图中当![]() 时
时![]() 的值得正负即可判断;③ 由函数开口方向可判断
的值得正负即可判断;③ 由函数开口方向可判断![]() 的正负,根据对称轴可判断
的正负,根据对称轴可判断![]() 的正负,再根据函数与
的正负,再根据函数与![]() 轴交点可得出
轴交点可得出![]() 的正负,即可得出答案;
的正负,即可得出答案;
④ 根据方程![]() 可以看做函数
可以看做函数![]() ,就相当于函数
,就相当于函数![]() (a 0)向下平移
(a 0)向下平移![]() 个单位长度,且与
个单位长度,且与![]() 有两个交点,即可得出答案.
有两个交点,即可得出答案.
解:① ∵ 函数与![]() 轴有两个交点,
轴有两个交点,
∴![]() ,所以① 错误;
,所以① 错误;
②∵ 当![]() 时,
时,![]() ,由图可知当
,由图可知当![]() ,
,![]() ,
,
∴![]() ,所以②错误;
,所以②错误;
③∵ 函数开口向上,
∴![]() ,
,
∵对称轴![]() ,
,![]() ,
,
∴![]() ,
,
∵函数与![]() 轴交于负半轴,
轴交于负半轴,
∴![]() ,
,
∴![]() ,所以③ 正确;
,所以③ 正确;
④方程![]() 可以看做函数
可以看做函数![]() 当y=0时也就是与
当y=0时也就是与![]() 轴交点,
轴交点,
∵方程有两个不相等的实数根,
∴函数![]() 与
与![]() 轴有两个交点
轴有两个交点
∵函数![]() 就相当于函数
就相当于函数![]() 向下平移
向下平移![]() 个单位长度
个单位长度
∴由图可知当函数![]() 向上平移大于2个单位长度时,交点不足2个,
向上平移大于2个单位长度时,交点不足2个,
∴![]() ,所以④错误.
,所以④错误.
正确答案为: ③

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目