题目内容
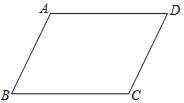
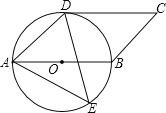
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°.
(1)试判断CD与⊙O的位置关系,并证明你的结论;
(2)若⊙O的半径为3,sin∠ADE=![]() ,求AE的值.
,求AE的值.
【答案】(1)CD与圆O相切;(2)AE=5.
【解析】
(1)连接OD,则∠AOD=为直角,由四边形ABCD是平行四边形,则AB∥CD,从而得出∠CDO=90°,即可证出答案;
(2)连接BE,则∠ADE=∠ABE,根据题意得sin∠ABE=![]() . 由AB是圆O的直径求出AB的长.再在Rt△ABE中,求得AE即可.
. 由AB是圆O的直径求出AB的长.再在Rt△ABE中,求得AE即可.
解:(1)CD与圆O相切. 证明:连接OD,则∠AOD=2∠AED =2×450=900
∵四边形ABCD是平行四边形,∴AB//DC
∴∠CDO=∠AOD=90°
∴OD⊥CD
∴CD与圆O相切
(2)连接BE,则∠ADE=∠ABE
∴sin∠ADE=sin∠ABE=![]()
∵AB是圆O的直径,∴∠AEB=900,AB=2×3=6
在Rt△ABE中,sin∠ABE=![]() .
.
∴AE=5 .

练习册系列答案
相关题目