题目内容
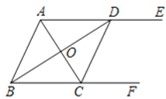
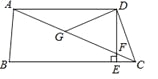
【题目】如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
根据直角三角形斜边上的中线的性质可得DG=AG,根据等腰三角形的性质可得∠ GAD=
∠ GDA,根据三角形外角的性质可得∠ CGD=2∠ GAD,再根据平行线的性质和等量关系可得∠ ACD=∠CGD,根据等腰三角形的性质可得CD=DG,再根据勾股定理即可求解.
∵DE⊥BC,
∴∠DEB=90°,
∵AD∥BC,
∴∠ADE+∠DEB=180°,
∴∠ADE=90°,
∵G为AF的中点,
∴DG=AG,
∴∠DAF=∠ADG,
∴∠DGC=∠DAF+∠ADG=2∠DAC,
∵AD∥BC,
∴∠ACB=∠DAC,
∵∠ACD=2∠ACB,
∴∠DGC=∠DCA,
∴DG=DC,
∵在Rt△DEC中,∠DEC=90°,DG=DC=3,CE=1,∴由勾股定理得:DE=![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目