Question

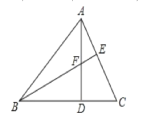
【题目】如图，在△ABC中，AD⊥BC，BE⊥AC，垂足分别为点D、E，AD与BE交于点F，BF=AC， ∠ABE=22°，则∠CAD的度数是________°.

Answer 1

【答案】23°.

【解析】

求出△DBF≌△DAC，根据全等三角形的性质得出AD=BD，求出∠ABD=∠DAB=45°，即可得出答案．

∵AD⊥BC，BE⊥AC，

∴∠BDF=∠ADC=90°,∠BEC=∠ADC=90°，

∴∠DAC+∠C=90°，∠DBF+∠C=90°，

∴∠DBF=∠DAC，

在△DBF和△DAC中

，

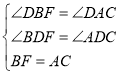∴△DBF≌△DAC，

∴AD=BD，

∵∠ADB=90°，

∴∠ABD=∠DAB=45°，

∵∠ABE=22°，

∴∠CAD=∠DBF=∠ABD∠ABE=45°22°=23°，

故答案为：23°.