题目内容
某超市经销一种销售成本为每件20元的商品.据市场调查分析,如果按每件30元销售,一周能售出500件,若销售单价每涨1元,每周的销售量就减少10件.设销售单价为每件x元(x≥30),一周的销售量为y件.
(1)写出y与x的函数关系式及自变量x的取值范围;
(2)该超市想通过销售这种商品一周获得利润8000元,销售单价应定为多少?
(1) y=800-10x(50≤x≤80);(2)40,60.
解析试题分析:(1)根据题意可得y=500-10(x-30).
(2)令y=8000,求出x的实际取值.
试题解析:(1)由题意得:
y=500-10(x-30)=800-10x(50≤x≤80)
(2)由题意得:-10x2+1000x-16000=8000
10x2-1000x+24000=0
x2-100x+2400=0
即(x-60)(x-40)=0
x1=60,x2=40
考点: 二次函数的应用.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
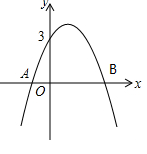

 经过A(
经过A( ,0)、B(5,0)两点,顶点为P.
,0)、B(5,0)两点,顶点为P. ,
, )和点D(
)和点D( ,
, )在该抛物线上,则当
)在该抛物线上,则当 时,
时, ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
 是抛物线上的一点,求△ABD的面积.
是抛物线上的一点,求△ABD的面积. 元,每售出一个小家电可获得的利润是多少元?(用含
元,每售出一个小家电可获得的利润是多少元?(用含