题目内容
为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担,李明按照相关政策投资销售本市生产的一种新型节能灯,已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=-10x+500.
⑴李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
⑵设李明获得的利润为W(元),当销售单价定为多少元时,每月可获得最大利润?
⑶物价部门规定,这种节能灯的销售单价不得高于25元,如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?
(1)600;(2)30;(3)500.
解析试题分析:(1)根据销售额=销售量×销售单价,列出函数关系式;
(2)用配方法将(2)的函数关系式变形,利用二次函数的性质求最大值;
(3)把y=3000代入(2)的函数关系式中,解一元二次方程求x,根据x的取值范围求x的值.
试题解析:⑴当x=20时,y=-10x+500=-10×20+500=300,
300×(12-10)=300×2=600,
即政府这个月为他承担的总差价为600元.
⑵依题意得,W=(x-10)(-10x+500)=-10x2+600x-5000=-10(x-30)2+4000
∵a=-10<0,∴当x=30时,W有最大值4000.
即当销售单价定为30元时,每月可获得最大利润4000元.
⑶由题意得:-10x2+600x-5000=3000,解得:x1=20,x2=40.
∵a=-10<0,抛物线开口向下,
∴结合图象可知:当20≤x≤40时,W≥3000.
又∵x≤25,
∴当20≤x≤25时,W≥3000.
设政府每个月为他承担的总差价为p元,
∴p=(12-10)×(-10x+500)
=-20x+1000.
∵k=-20<0.
∴p随x的增大而减小,∴当x=25时,p有最小值500.
即销售单价定为25元时,政府每个月为他承担的总差价最少为500元.
考点: 二次函数的应用.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案某商家独家销售具有地方特色的某种商品,每件进价为40元.经过市场调查,一周的销售量y件与销售单价x(x≥50)元/件的关系如下表:
| 销售单价x (元/件) | … | 55 | 60 | 70 | 75 | … |
| 一周的销售量y (件) | … | 450 | 400 | 300 | 250 | … |
(2)设一周的销售利润为S元,请求出S与x的函数关系式,并确定当销售单价在什么范围内变化时,一周的销售利润随着销售单价的增大而增大?
(3)雅安地震牵动亿万人民的心,商家决定将商品一周的销售利润全部寄往灾区,在商家购进该商品的贷款不超过10000元情况下,请你求出该商家最大捐款数额是多少元?
 与抛物线
与抛物线 交于A、B两点,
交于A、B两点, 时,在直线AB下方的抛物线上求点P,使△ABP的面积等于5;
时,在直线AB下方的抛物线上求点P,使△ABP的面积等于5;
 .等腰直角△EFG中,EF=4, ∠EGF=45°,且△EFG与□ABCD位于直线AD的同侧,点F与点D重合,GF与AD在同一直线上.△EFG从点D出发以每秒1个单位的速度沿射线DA方向平移,当点G到点A时停止运动;同时点P也从点A出发,以每秒3个单位的速度沿折线AD→DC方向运动,到达点C时停止运动,设运动的时间为t.
.等腰直角△EFG中,EF=4, ∠EGF=45°,且△EFG与□ABCD位于直线AD的同侧,点F与点D重合,GF与AD在同一直线上.△EFG从点D出发以每秒1个单位的速度沿射线DA方向平移,当点G到点A时停止运动;同时点P也从点A出发,以每秒3个单位的速度沿折线AD→DC方向运动,到达点C时停止运动,设运动的时间为t. 的长度;
的长度; 平移的过程中,记
平移的过程中,记 相互重叠的面积为
相互重叠的面积为 ,请直接写出面积
,请直接写出面积 的函数关系式,并写出
的函数关系式,并写出 与线段
与线段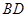 交于点
交于点 ,连接
,连接 .是否存在这样的时间
.是否存在这样的时间 为等腰三角形?若存在,求出对应的
为等腰三角形?若存在,求出对应的

 ),当t =4秒时:
),当t =4秒时:
 (5m2-2m+13)="0" (m为常数)的两个实数根,点M在抛物线上,连接MQ、MH、PM,且.MP平分∠QMH,求出t值及点M的坐标.
(5m2-2m+13)="0" (m为常数)的两个实数根,点M在抛物线上,连接MQ、MH、PM,且.MP平分∠QMH,求出t值及点M的坐标.

