题目内容
某个体户春节前代理销售某种品牌的酒,已知进价为每件40元,生产厂家要求销售价不少于40元,且不大于70元,市场调查发现:若每件以50元销售,平均每天可销售90件,价格每降低1元,平均每天多销售3件,价格每升高1元,平均每天少销售3件.
(1)写出平均每天销售量y(件)与每件销售价x(元)之间的函数关系式,并注明自变量的取值范围;
(2)求出该个体户每天销售这种酒的毛利润W(元)与每件酒的售价x(元)之间的函数关系式,并注明自变量的取值范围(每件的毛利润=售价-进价);
(3)当酒的售价为多少时平均每天的利润最大,最大利润是多少?
(1)y=-3x+240,其中40≤x≤70;(2)W=-3x2+360x-9600,其中40≤x≤70;(3)60,1200元.
解析试题分析:(1)每件销售价x则降低了(50-x)元,销售量是90+3(50-x)件;或升高了(x-50)元,销售量是90-3(x-50)件,两个式子可以统一,根据销售价的范围写出自变量的取值范围;
(2)每天的利润=每件的利润×销售量,每件利润为(x-40)元,销售量为y,所以利润表达式w=(x-40)(-3x+240);
(3)运用函数性质求解.
试题解析:(1)y=-3(x-50)+90,
即y=-3x+240,其中40≤x≤70;
(2)W=x(-3x+240)-40(-3x+240),
W=-3x2+360x-9600,其中40≤x≤70;
(3)W=-3(x-60)2+1200
当x=60时,W有最大值1200.
答:当酒的售价为60元时,平均每天的毛利润最大,最大毛利润为1200元.
考点: 二次函数的应用.

某商家独家销售具有地方特色的某种商品,每件进价为40元.经过市场调查,一周的销售量y件与销售单价x(x≥50)元/件的关系如下表:
| 销售单价x (元/件) | … | 55 | 60 | 70 | 75 | … |
| 一周的销售量y (件) | … | 450 | 400 | 300 | 250 | … |
(2)设一周的销售利润为S元,请求出S与x的函数关系式,并确定当销售单价在什么范围内变化时,一周的销售利润随着销售单价的增大而增大?
(3)雅安地震牵动亿万人民的心,商家决定将商品一周的销售利润全部寄往灾区,在商家购进该商品的贷款不超过10000元情况下,请你求出该商家最大捐款数额是多少元?


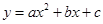 过A、B、C三点,AB=10,tan∠CAD=
过A、B、C三点,AB=10,tan∠CAD= .
. 坐标为(2,4),直线x=2与
坐标为(2,4),直线x=2与 轴相交于点
轴相交于点 ,连结
,连结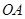 ,抛物线y=x
,抛物线y=x
 从点
从点 沿
沿 ,顶点
,顶点 到
到
 ,
, 最短;
最短; ,使△
,使△ 的面积与△
的面积与△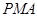 的面积相等,若存在,请求出点
的面积相等,若存在,请求出点