题目内容
如图,点 是等边
是等边 内一点,
内一点, ,
,  .将
.将 绕点
绕点 按顺时针方向旋转
按顺时针方向旋转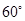 得
得 ,连接
,连接 .
.
(1)当 ,
, 时,试判断
时,试判断 的形状,并说明理由.
的形状,并说明理由.
(2)请写出 是等边三角形时
是等边三角形时 、
、 的度数.
的度数.
 = 度;
= 度;  = 度.
= 度.
(3)探究:若 ,则
,则 为多少度时,
为多少度时, 是等腰三角形?
是等腰三角形?
(只要写出探究结果) = ;
= ;
 是等边
是等边 内一点,
内一点, ,
,  .将
.将 绕点
绕点 按顺时针方向旋转
按顺时针方向旋转 得
得 ,连接
,连接 .
.
(1)当
 ,
, 时,试判断
时,试判断 的形状,并说明理由.
的形状,并说明理由.(2)请写出
 是等边三角形时
是等边三角形时 、
、 的度数.
的度数. = 度;
= 度;  = 度.
= 度.(3)探究:若
 ,则
,则 为多少度时,
为多少度时, 是等腰三角形?
是等腰三角形?(只要写出探究结果)
 = ;
= ;(1) 是直角三角形.(2)
是直角三角形.(2) = 120 度;
= 120 度;  = 120 度.
= 120 度.
(3) =
= 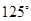 或
或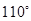 或
或 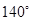
 是直角三角形.(2)
是直角三角形.(2) = 120 度;
= 120 度;  = 120 度.
= 120 度. (3)
 =
= 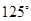 或
或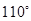 或
或 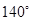
试题分析:(1)
结论:
 是直角三角形,
是直角三角形,
证明:由题意可得:△ACD≌△BCO,
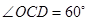 ,
,∴CO=CD,
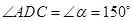 ,
,∴△OCD是等边三角形,
∴
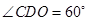 ,
,∴
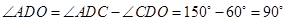 ,
, ∴
 是直角三角形.
是直角三角形.(2)由题意可得:△ACD≌△BCO,
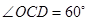 ,
,∴CO=CD,
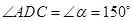 ,
,∴△OCD是等边三角形,
∴
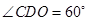
 是等边三角形,所以
是等边三角形,所以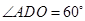
因此
 =
=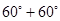 = 120 度;
= 120 度;因为三角形AOD、COD都是等边三角形,所以
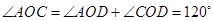
而
 =
=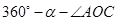 = 120 度.
= 120 度. (3) 由(1)知△OCD是等边三角形,那么OC=OD=CD,
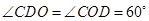 ;若
;若
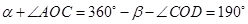 ;根据旋转的特征
;根据旋转的特征 ;在三角形AOD中,根据三角形内角和定理
;在三角形AOD中,根据三角形内角和定理 ,那么
,那么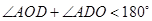 ,要使
,要使 是等腰三角形,所以
是等腰三角形,所以 =
= 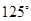 或
或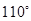 或
或 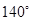 ;
; 点评:本题考查平等边三角形和旋转,熟悉等边三角形的性质和旋转的概念和特征是解本题的关键

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目






 C;平移△ABC,若A的对应点
C;平移△ABC,若A的对应点 的坐标为(0,4),画出平移后对应的△
的坐标为(0,4),画出平移后对应的△ ;
; 轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
 的坐标是 .
的坐标是 .