题目内容
【题目】如图，矩形OABC中，O是原点，OA＝8，AB＝6，则对角线AC和BO的交点H的坐标为.
【答案】
【解析】解 ：过点H 作HE⊥OA与E，HF⊥OC于点F,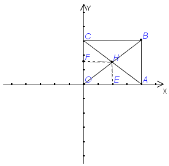 
∵ 四边形OABC为矩形
∴ OH=HB AH=HC AB=OC OA=BC
∵ HE⊥OA BA⊥OA
∴ HE∥BA
∴ OH∶HB=OE∶EA
∵ OH=HB
∴ OE=EA
∵ OA=8
∴ OE=
×OA=4
同理可得到OF=×OC=3,
故点H的坐标为(4,3)
故答案为 ：（4,3）
根据矩形的对边相等，对角线互相平分得出 OH=HB AH=HC AB=OC OA=BC，根据同一平面内垂直于同一直线的两条直线互相平行得出 HE∥BA，根据平行线分线段成比例定理得出 OH∶HB=OE∶EA，根据OH=HB，从而得到OE=EA，根据OA的长度，进而求出OE的长，同理得出OF的长，进而得出H点的坐标。
练习册系列答案
相关题目
