Question

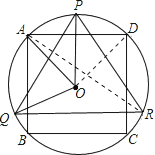
【题目】如图，△PQR是⊙O的内接正三角形，四边形ABCD是⊙O的内接正方形，BC∥QR，则∠AOQ= ____________．

Answer 1

【答案】75°．

【解析】作辅助线连接OD，根据题意求出∠POQ和∠AOD的，利用平行关系求出∠AOP度数，即可求出∠AOQ的度数．

解：连接OD，AR，

∵△PQR是⊙O的内接正三角形，
∴∠PRQ=60°，
∴∠POQ=2×∠PRQ=120°，
∵四边形ABCD是⊙O的内接正方形，
∴△AOD为等腰直角三角形，
∴∠AOD=90°，
∵BC∥RQ，AD∥BC，
∴AD∥QR，
∴∠ARQ=∠DAR，
∴弧AQ=弧DR，
∵△PQR是等边三角形，
∴PQ=PR，
∴弧PQ=弧PR，
∴弧AP=弧PD，
∴∠AOP=∠AOD=45°，
所以∠AOQ=∠POQ-∠AOP=120°-45°=75°．