题目内容
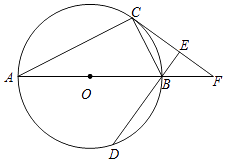
【题目】如图,点P是⊙O外一点,过点P作⊙O的切线PA,切点为A,连接PO,延长PO交⊙O于点B,若∠P=30°,PA=3 ![]() ,则弧AB的长为 .
,则弧AB的长为 . 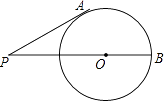
【答案】2π
【解析】解:如图,连接OA,
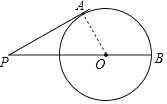
∵PA与⊙O相切,
∴∠OAP=90°,
在Rt△PAO中,∵∠P=30°,PA=3 ![]() ,
,
∴∠AOP=60°,OA=PAtan∠P=3 ![]() ×
× ![]() =3,
=3,
∴∠AOB=120°,
则弧AB的长为 ![]() =2π,
=2π,
所以答案是:2π.
【考点精析】关于本题考查的切线的性质定理和弧长计算公式,需要了解切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的才能得出正确答案.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目