ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌЕШбќШ§НЧаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌADЮЊЕзБпBCЩЯЕФИпЃЌЖЏЕу
ЃЌADЮЊЕзБпBCЩЯЕФИпЃЌЖЏЕу![]() ДгЕуDГіЗЂЃЌбиDAЗНЯђдШЫйдЫЖЏЃЌЫйЖШЮЊ
ДгЕуDГіЗЂЃЌбиDAЗНЯђдШЫйдЫЖЏЃЌЫйЖШЮЊ![]() ЃЌдЫЖЏЕН
ЃЌдЫЖЏЕН![]() ЕуЭЃжЙЃЌЩшдЫЖЏЪБМфЮЊ
ЕуЭЃжЙЃЌЩшдЫЖЏЪБМфЮЊ![]() ЃЌСЌНгBPЃЎ(0ЁмtЁм8)
ЃЌСЌНгBPЃЎ(0ЁмtЁм8)
ЃЈ1ЃЉЧѓADЕФГЄЃЛ
ЃЈ2ЃЉЩшЁїAPBЕФУцЛ§ЮЊyЃЈcmЃЉЃЌЧѓyгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉЪЧЗёДцдкФГвЛЪБПЬtЃЌЪЙЕУSЁїAPB:SЁїABC=1:3ЃЌШєДцдкЃЌЧѓГі![]() ЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЃЈ4ЃЉЪЧЗёДцдкФГвЛЪБПЬ![]() ЃЌЪЙЕУЕуPдкЯпЖЮABЕФДЙжБЦНЗжЯпЩЯЃЌШєДцдкЃЌЧѓГі
ЃЌЪЙЕУЕуPдкЯпЖЮABЕФДЙжБЦНЗжЯпЩЯЃЌШєДцдкЃЌЧѓГі![]() ЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ8ЃЛЃЈ2ЃЉyЃН24Љ3tЃЈ0ЁмtЁм8ЃЉЃЛЃЈ3ЃЉДцдкЃЌ![]() ЃЛЃЈ4ЃЉДцдкЃЌ
ЃЛЃЈ4ЃЉДцдкЃЌ![]()
ЁОНтЮіЁП
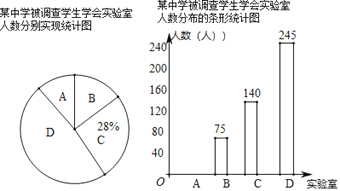
ЃЈ1ЃЉРћгУЕШбќШ§НЧаЮЕФаджЪвдМАЙДЙЩЖЈРэНтОіЮЪЬтМДПЩЃЎ
ЃЈ2ЃЉИљОнyЃНSЁїAPBЃНSЁїABDЉSЁїPBDЃЌЛЏМђМЦЫуМДПЩЃЎ
ЃЈ3ЃЉгЩЬтвтSЁїAPBЃКSЁїABCЃН1ЃК3ЃЌЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЎ
ЃЈ4ЃЉгЩЬтвтЕуPдкЯпЖЮABЕФДЙжБЦНЗжЯпЩЯЃЌЭЦГіPAЃНPBЃЌдкRtЁїPBDжаЃЌИљОнPB2ЃНPD2+BD2ЃЌЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЎ
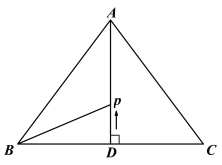
ЃЈ1ЃЉЁпABЃНACЃЌADЁЭBCЃЌ
ЁрBCЃНDCЃН6cmЃЌ
дкRtЁїABDжаЃЌЁпЁЯADBЃН90ЁуЃЌABЃН10cmЃЌBDЃН6cmЃЌ
ЁрADЃН![]() ЃН
ЃН![]() ЃН8ЃЈcmЃЉЃЎ
ЃН8ЃЈcmЃЉЃЎ
ЃЈ2ЃЉyЃНSЁїAPBЃНSЁїABDЉSЁїPBDЃН![]() ЁС6ЁС8Љ
ЁС6ЁС8Љ![]() ЁС6ЁСtЃНЉ3t+24ЃЎ
ЁС6ЁСtЃНЉ3t+24ЃЎ
ЁрyЃН24Љ3tЃЈ0ЁмtЁм8ЃЉЃЎ
ЃЈ3ЃЉЁпSЁїAPBЃКSЁїABCЃН1ЃК3ЃЌ
ЁрЃЈ24Љ3tЃЉЃК![]() ЁС12ЁС8ЃН1ЃК3ЃЌ
ЁС12ЁС8ЃН1ЃК3ЃЌ
НтЕУtЃН![]() ЃЎ
ЃЎ
ЁрТњзуЬѕМўЕФtЕФжЕЮЊ![]() ЃЎ
ЃЎ
ЃЈ4ЃЉгЩЬтвтЕуPдкЯпЖЮABЕФДЙжБЦНЗжЯпЩЯЃЌ
ЁрPAЃНPBЃЌ
дкRtЁїPBDжаЃЌЁпPB2ЃНPD2+BD2ЃЌ
Ёрt2ЃНЃЈ8ЉtЃЉ2+62ЃЌ
НтЕУtЃН![]() ЃЎ
ЃЎ
ЁрТњзуЬѕМўЕФtЕФжЕЮЊ![]() ЃЎ
ЃЎ

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ