题目内容
【题目】点A,C,为半径是6的⊙O上两点,点B为![]() 的中点,以线段BA,BC为邻边作菱形ABCD,使点D落在⊙O内(不含圆周上),则下列结论:①直线BD必过圆心O;②菱形ABCD的边长a的取值范围是0<a<10;③若点D与圆心O重合,则∠ABC=120°;④若DO=2,则菱形ABCD的边长为
的中点,以线段BA,BC为邻边作菱形ABCD,使点D落在⊙O内(不含圆周上),则下列结论:①直线BD必过圆心O;②菱形ABCD的边长a的取值范围是0<a<10;③若点D与圆心O重合,则∠ABC=120°;④若DO=2,则菱形ABCD的边长为![]() 或
或![]() .其中正确的是( )
.其中正确的是( )
A. ①③ B. ②③④ C. ①③④ D. ①②③④
【答案】A
【解析】
①根据垂径定理的推论即可解决问题;
②当BD是直径时,边长最大,最大值为6![]() ,故②错误;
,故②错误;
③如图2中,当点D与点O重合时,易知△ABO,△BOC都是等边三角形,由此即可解决问题;
④分两种情形分别求解即可判定;
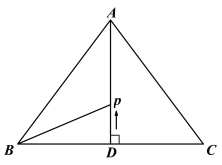
如图1中,连接AC、BD交于点K.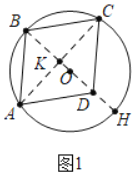
∵四边形ABCD是菱形,
∴BD垂直平分线段AC,
∴直线BD经过圆心O,设直线BD交⊙O于H.故①正确,
当BD是直径时,边长最大,最大值为6![]() ,故②错误,
,故②错误,
如图2中,当点D与点O重合时,易知△ABO,△BOC都是等边三角形,
∴∠ABO=∠CBO=60°,
∴∠ABC=120°.故③正确,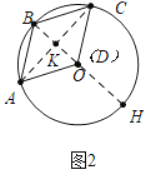
如图3中,当点D在BO的延长线上时,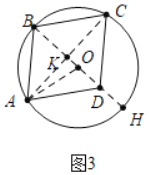
∵OD=2,OB=6,
∴BD=8,
∴BK=DK=4,OK=2,
∴AK2=OA2-OK2=32,
AB=![]() ,
,
当点D在线段OB上时,同法可得AB=2![]() ,
,
∴AB=4![]() 或2
或2![]() ,故④错误;
,故④错误;
故选:A.

练习册系列答案
相关题目