题目内容
【题目】已知,PA、PB是⊙O的切线,切点分别为A、B,AC是⊙O的直径.
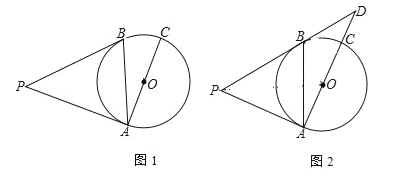
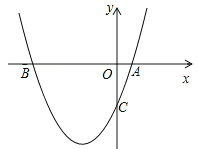
(1)如图1,若∠BAC=25°,求∠P的度数;
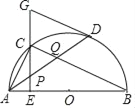
(2)如图2,延长PB、AC相交于点D.若AP=AC,求cosD的值.
【答案】(1)50°;(2)cosD=![]() .
.
【解析】
(1)连接OB.根据平行的想得到PA⊥AO,PB⊥OB,根据四边形的内角和即可得到结论;
(2)连结OP交AB于点E,再连OB、BC,根据切线的性质得到∠PAC=∠PBO=90°,推出OP是AB的垂直平分线,根据相似三角形的性质即可得到结论.
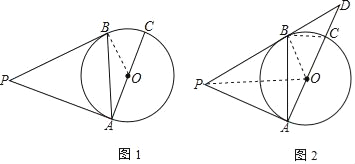
(1)证明:如图1,连接OB.
∵PA、PB分别切⊙O于A、B两点,
∴PA⊥AO,PB⊥OB,
∴∠PAO=∠PBO=90°.
∵∠BAC=25°,OB=OA,
∴∠BOA=180°﹣25°﹣25°=130°,
∴∠P=360°﹣90°﹣90°﹣130°=50°;
(2)解:如图2,连结OP交AB于点E,再连OB、BC,
∵PA、PB是⊙O的切线,
∴∠PAC=∠PBO=90°,
∵AP=AC,AC是⊙O的直径,
∴![]() ,∵PB=PA,OB=OA,
,∵PB=PA,OB=OA,
∴OP是AB的垂直平分线,
∵∠OAP=90°,AE⊥OP,
∴△OEA∽△AEP∽△OAP,
∴![]() ,
,
设OE=a,可得AE=BE=BC=2a,PE=4a,
∴OP=5a,
∴OA=![]() a,PA=PB=2
a,PA=PB=2![]() a,
a,
∵∠ABC=∠AEO=90°,
∴OP∥BC,
∴△DBC∽△DPO,
∴![]() =
=![]() =
=![]() =
=![]() .
.
∴BD=![]() ,OD=
,OD=![]()
![]() a,
a,
∴COSD=![]() =
=![]() .
.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目