题目内容
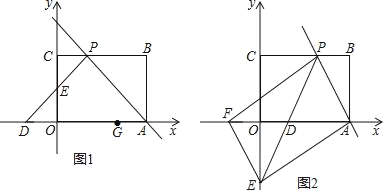
【题目】如图①，在
中，
平分
（
），
为上一点，且
于点
.
（1）当
，
时，求
的度数；
（2）若
，
，请结合（1）的计算猜想、
、
之间的数量关系，直接写出答案，不说明理由；（用含有
、
的式子表示）
（3）如图②，当点在的延长线上时，其余条件不变，则（2）中的结论还成立吗？若成立，请说明为什么；若不成立，请写出成立的结论，并说明为什么.
【答案】（1）
；（2）
；（3）成立. ，理由见解析.
【解析】
（1）根据三角形的内角和定理求出∠BAC，再根据角平分线的定义求出∠BAE，然后根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解；
（2）根据三角形的内角和定理和角平分线的定义表示出∠BAE，再根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠AEC，然后根据直角三角形两锐角互余列式整理即可得解；
（3）结论仍然成立．根据（2）可以得到∠AEC=90°+
（∠B-∠C），根据对顶角相等即可求得∠DEF，然后利用直角三角形的两个锐角互余即可求解．
（1）∵
，
（已知）
（三角形的内角和等于
）
∴
（等量代换）
∵
平分
（已知）
∴
（角平分线的定义）
∴
（三角形的一个外角等于和它不相邻的两个内角的和）
，即
.
∵
于点
（已知）
∴
（垂直的定义）
∴
（直角三角形的两个锐角互余）
∴
（等量代换）
（2）
（3）成立. 
理由：∵
，
（已知）
（三角形的内角和等于）
∴
（等量代换）
∵平分（已知）
∴
（角平分线的定义）
∴
（三角形的一个外角等于和它不相邻的两个内角的和）
∴
（对顶角相等）
∵于点（已知）
∴（垂直的定义）
∴（直角三角形的两个锐角互余 ）
∴（等量代换）
练习册系列答案
阅读快车系列答案
相关题目
