Question

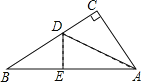
【题目】直线 AB∥CD，直线 a 分别交 AB、CD 于点 E、F，点 M 在线段 EF 上，点 P 是 直线 CD 上的一个动点(点 P 不与点 F 重合)．

(1)如图 1，当点 P 在射线 FC 上移动时，∠FMP＋∠FPM 与∠AEF 有什么数量关系？ 请说明理由；

(2)如图 2，当点 P 在射线 FD 上移动时，∠FMP＋∠FPM 与∠AEF 有什么数量关系？ 请说明理由．

Answer 1

【答案】（1）∠AEF=∠MPF+∠FPM；（2）∠FMP+∠FPM+∠AEF=180°；

【解析】

（1）由AB∥CD，利用两直线平行，同旁内角互补，可得∠AEF十∠EFC=180°，又由三角形内角和定理，即可得∠FMP+∠FPM+∠EFC=180°，则可得∠FMP+∠FPM=∠AEF；

（2）由AB∥CD，利用两直线平行，内错角相等，即可证得∠AEF=∠EFD，又由三角形内角和定理，即可得∠FMP+∠FPM+∠EFD=180°，则可得∠FMP+∠FPM+∠AEF=180°．

(1)∠FMP+∠FPM=∠AEF，

理由：∵AB∥CD，

∴∠AEF=∠DFM，

又∵∠FMP+∠FPM=∠DFM，

∴∠FMP+∠FPM=∠AEF；

(2)∠FMP+∠FPM与∠AEF互补(或∠FMP+∠FPM+∠AEF=180)…(8分)

理由：∵AB∥CD，

∴∠AEF=∠EFD(两直线平行,内错角相等)，

∵∠FMP+∠FPM+∠EFD=180(三角形内角和定理)，

∴∠FMP+∠FPM+∠AEF=180(等量代换).