题目内容
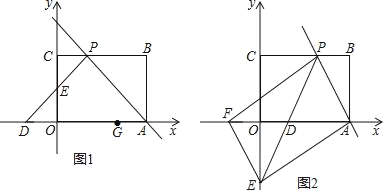
【题目】如图1,矩形OABC摆放在平面直角坐标系中,点A在x轴上,点C在y轴上,OA=3,OC=2,过点A的直线交矩形OABC的边BC于点P,且点P不与点B、C重合,过点P作∠CPD=∠APB,PD交x轴于点D,交y轴于点E.
(1)若△APD为等腰直角三角形.
①求直线AP的函数解析式;
②在x轴上另有一点G的坐标为(2,0),请在直线AP和y轴上分别找一点M、N,使△GMN的周长最小,并求出此时点N的坐标和△GMN周长的最小值.
(2)如图2,过点E作EF∥AP交x轴于点F,若以A、P、E、F为顶点的四边形是平行四边形,求直线PE的解析式.
【答案】(1)①y=﹣x+3,②N(0,![]() ),
),![]() ;(2) y=2x﹣2.
;(2) y=2x﹣2.
【解析】
(1)①由矩形的性质和等腰直角三角形的性质可求得∠BAP=∠BPA=45°,从而可得BP=AB=2,进而得到点P的坐标,再根据A、P两点的坐标从而可求AP的函数解析式;
②作G点关于y轴对称点G'(﹣2,0),作点G关于直线AP对称点G'(3,1),连接G'G'交y轴于N,交直线AP 于M,此时△GMN周长的最小,根据点G'、G'两点的坐标,求出其解析式,然后再根据一次函数的性质即可求解;
(2)根据矩形的性质以及已知条件求得PD=PA,进而求得DM=AM,根据平行四边形的性质得出PD=DE,然后通过得出△PDM≌△EDO得出点E和点P的坐标,即可求得.
解:(1)①∵矩形OABC,OA=3,OC=2,
∴A(3,0),C(0,2),B(3,2),
AO∥BC,AO=BC=3,∠B=90°,CO=AB=2,
∵△APD为等腰直角三角形,
∴∠PAD=45°,
∵AO∥BC,
∴∠BPA=∠PAD=45°,
∵∠B=90°,
∴∠BAP=∠BPA=45°,
∴BP=AB=2,
∴P(1,2),
设直线AP解析式y=kx+b,
∵过点A,点P,
∴![]()
∴![]() ,
,
∴直线AP解析式y=﹣x+3;
②如图所示:
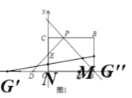
作G点关于y轴对称点G'(﹣2,0),作点G关于直线AP对称点G'(3,1)
连接G'G'交y轴于N,交直线AP 于M,此时△GMN周长的最小,
∵G'(﹣2,0),G'(3,1)
∴直线G'G'解析式y=![]() x+
x+![]()
当x=0时,y=![]() ,
,
∴N(0,![]() ),
),
∵G'G'![]() =
=![]() ,
,
∴△GMN周长的最小值为![]() ;
;
(2)如图:作PM⊥AD于M,
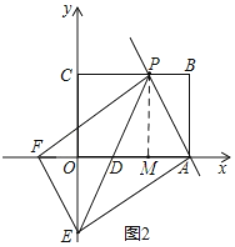
∵BC∥OA
∴∠CPD=∠PDA且∠CPD=∠APB,
∴PD=PA,且PM⊥AD,
∴DM=AM,
∵四边形PAEF是平行四边形
∴PD=DE
又∵∠PMD=∠DOE,∠ODE=∠PDM
∴△PMD≌△EOD,
∴OD=DM,OE=PM,
∴OD=DM=MA,
∵PM=2,OA=3,
∴OE=2,OM=2
∴E(0,﹣2),P(2,2)
设直线PE的解析式y=mx+n
![]()
∴![]()
∴直线PE解析式y=2x﹣2.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD对折,使它落在斜边AB上,且与AE重合,则CD等于( )
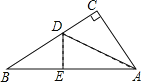
A. 3cmB. 4cmC. 5cmD. 6cm
【题目】先填写表,通过观察后再回答问题:
a | …… | 0.0001 | 0.01 | 1 | 100 | 10000 | …… |
| …… | 0.01 | x | 1 | y | 100 | …… |
(1)表格中,x=_________,y=_________
(2)从表格中探究a与![]() 数位的规律,并利用这个规律解决下面两个问题:
数位的规律,并利用这个规律解决下面两个问题:
①已知![]() ,则
,则![]() ≈___________
≈___________
②已知![]() ,若
,若![]() ,用含m的代数式表示b,则b=___________
,用含m的代数式表示b,则b=___________
(3)试比较![]() 与a的大小(直接写出结果)
与a的大小(直接写出结果)