题目内容
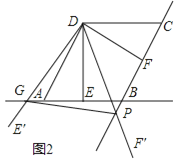
【题目】如图,Rt△ABC中,AC⊥BC,AE=AO,BF=BO,则∠EOF的度数是_____.

【答案】45°
【解析】
先根据直角三角形的性质可求∠A+∠B=90°,再根据三角形内角和可得:∠A+∠B+∠AEO+∠AOE+∠BOF+∠BFO=360°,继而求出∠AEO+∠AOE+∠BOF+∠BFO=270°,
根据AE=AO,BF=BO,可得∠AEO=∠AOE,∠BOF=∠BFO,继而可得2∠AOE+2∠BOF =270°,因此∠AOE+∠BOF =135°,最后根据补角可求出∠EOF.
因为AC⊥BC,
所以∠C=90°,
所以∠A+∠B=90°,
由三角形内角和可得:∠A+∠AEO+∠AOE=180°,∠B +∠BOF+∠BFO=180°,
所以∠A+∠B+∠AEO+∠AOE+∠BOF+∠BFO=360°,
所以∠AEO+∠AOE+∠BOF+∠BFO=270°,
因为AE=AO,BF=BO,
所以∠AEO=∠AOE,∠BOF=∠BFO,
所以 2∠AOE+2∠BOF =270°,
所以∠AOE+∠BOF =135°,
所以∠EOF=180°-135°=45°.
故答案为:45°.

练习册系列答案
相关题目