题目内容
【题目】如图,正方形ABCD中,E为DC边上一点,且DE=1,AE=EF,∠AEF=90°,则FC= ( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
【答案】B
【解析】分析:如图,过点F作FM⊥DC,交DC的延长线于点M,根据已知条件证得△ADE≌△EFM,利用全等三角形的性质易得FM=CM=1,根据勾股定理即可求得FC的长.
详解:
如图,过点F作FM⊥DC,交DC的延长线于点M,
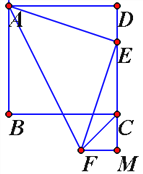
∵四边形ABCD为正方形,
∴AD=CD,∠D=90°,
∵∠AEF=90°,
∴∠DAE+∠AED=∠FEM+∠AED=90°,
∴∠DAE =∠FEM,
在△ADE和△EFM中,
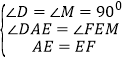 ,
,
∴△ADE≌△EFM,
∴DE=FM=1,AD=EM,
∵AD=CD,
∴CD=EM,
∴DE=CM=1.
在Rt△FCM中,根据勾股定理求得FC=![]() .
.
故选B.

练习册系列答案
相关题目