题目内容
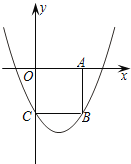
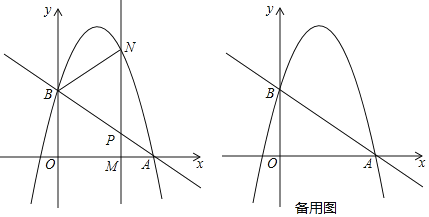
【题目】如图,直线y=﹣![]() x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣
x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过点A,B,M(m,0)为x轴上一动点,点M在线段OA上运动且不与O,A重合,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
x2+bx+c经过点A,B,M(m,0)为x轴上一动点,点M在线段OA上运动且不与O,A重合,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
(1)求点B的坐标和抛物线的解析式;
(2)在运动过程中,若点P为线段MN的中点,求m的值;
(3)在运动过程中,若以B,P,N为顶点的三角形与△APM相似,求点M的坐标;
【答案】(1)B(0,2),抛物线解析式为y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)m的值为![]() ;
;
(3)当以B,P,N为顶点的三角形与△APM相似时,点M的坐标为(2.5.0)或(![]() ,0).
,0).
【解析】
(1)把A点坐标代入直线解析式可求得c,则可求得B点坐标,由A、B的坐标,利用待定系数法可求得抛物线解析式;
(2)用m可表示出M、P、N的坐标,由题意可知有P为线段MN的中点,可得到关于m的方程,可求得m的值.
(3)由M点坐标可表示P、N的坐标,从而可表示出MA、MP、PN、PB的长,分∠NBP=90°和∠BNP=90°两种情况,分别利用相似三角形的性质可得到关于m的方程,可求得m的值,从而得到点M的坐标.
(1)∵y=﹣![]() x+c与x轴交于点A(3,0),与y轴交于点B,
x+c与x轴交于点A(3,0),与y轴交于点B,
∴0=﹣2+c,解得c=2,
∴B(0,2),
∵抛物线y=﹣![]() x2+bx+c经过点A,B,
x2+bx+c经过点A,B,
∴![]() ,解得
,解得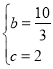 ,
,
∴抛物线解析式为y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)由(1)可知直线解析式为y=﹣![]() x+2,
x+2,
∵M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N,
∴P(m,﹣![]() m+2),N(m,﹣
m+2),N(m,﹣![]() m2+
m2+![]() m+2),
m+2),
∵P为线段MN的中点时,
∴有2(﹣![]() m+2)=﹣
m+2)=﹣![]() m2+
m2+![]() m+2,
m+2,
解得m=3(三点重合,舍去)或m=![]() .
.
故m的值为![]() .
.
(3)由(1)可知直线解析式为y=﹣![]() x+2,
x+2,
∵M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N,
∴P(m,﹣![]() m+2),N(m,﹣
m+2),N(m,﹣![]() m2+
m2+![]() m+2),
m+2),
∴PM=﹣![]() m+2,AM=3﹣m,PN=﹣
m+2,AM=3﹣m,PN=﹣![]() m2+
m2+![]() m+2﹣(﹣
m+2﹣(﹣![]() m+2)=﹣
m+2)=﹣![]() m2+4m,
m2+4m,
∵△BPN和△APM相似,且∠BPN=∠APM,
∴∠BNP=∠AMP=90°或∠NBP=∠AMP=90°,
当∠BNP=90°时,则有BN⊥MN,
∴N点的纵坐标为2,
∴﹣![]() m2+
m2+![]() m+2=2,解得m=0(舍去)或m=2.5,
m+2=2,解得m=0(舍去)或m=2.5,
∴M(2.5,0);
当∠NBP=90°时,过点N作NC⊥y轴于点C,
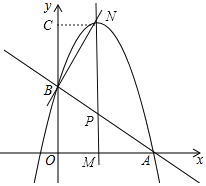
则∠NBC+∠BNC=90°,NC=m,BC=﹣![]() m2+
m2+![]() m+2﹣2=﹣
m+2﹣2=﹣![]() m2+
m2+![]() m,
m,
∵∠NBP=90°,
∴∠NBC+∠ABO=90°,
∴∠ABO=∠BNC,
∴Rt△NCB∽Rt△BOA,
∴![]() ,
,
∴![]() =
=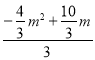 ,解得m=0(舍去)或m=
,解得m=0(舍去)或m=![]() ,
,
∴M(![]() ,0);
,0);
综上可知,当以B,P,N为顶点的三角形与△APM相似时,点M的坐标为(2.5.0)或(![]() ,0).
,0).

【题目】为响应垃圾分类处理,改善生态环境,某小区将生活垃圾分成三类:厨余垃圾、可回收垃圾和其他垃圾,分别记为a,b,c,并且设置了相应的垃圾箱,“厨余垃圾”箱,“可回收垃圾”箱和“其他垃圾”箱,分别记为A,B,C
(1)小明将垃圾分装在三个袋中,任意投放,用画树状图或列表的方法求把三个袋子都放错位置的概率是多少?
(2)某学习小组为了了解居民生活垃圾分类投放的情况,现随机抽取了某天三类垃圾箱中总共100吨的生活垃圾,数据统计如表(单位:吨):
A | B | C | |
a | 40 | 10 | 10 |
b | 3 | 24 | 3 |
c | 2 | 2 | 6 |
调查发现,在“可回收垃圾”中塑料类垃圾占10%,每回收1吨塑料类垃圾可获得0.7吨二级原料,某城市每天大约产生200吨生活垃圾假设该城市每天处理投放正确的垃圾,每天大概可回收多少吨塑料类垃圾的二级原料?