Question

【题目】等腰中，，点是上一点(与不重合)，连接,将线段绕点顺时针旋转，得到线段.连接. 探究的度数，以及线段与的数量关系.

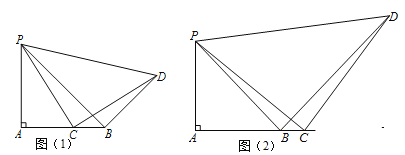
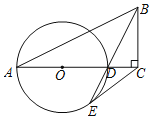
(1)尝试探究:如图(1) ； ；

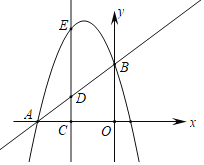
(2)类比探索:如图(2)，点在直线上，且在点右侧，还能得出与(1)中同样的结论么?请写出你得到的结论并证明:

Answer 1

【答案】（1），；（2）结论：， ，理由详见解析

【解析】

（1）由题意得：△PCD为等腰直角三角形，且∠PCD=90°则∠CPD=45°=∠APB，证明△PAC∽△PBD，得出∠PBD=∠PAC=90°，，因此，即可得出结论；

（2）由题意得：△PCD为等腰直角三角形，且∠PCD=90°则∠CPD=45°=∠APB，证明△PAC∽△PBD，得出∠PBD=∠PAC=90°，，因此，即可得出结论.

解：（1）为等腰直角三角形，且，

，

，即，

又，

，相似比为，

，

∴，

∴，

故答案为：，，

（2）结论：； ；理由如下：

为等腰直角三角形，且，

，

，即，

又，

，相似比为，

， ，

，

.