题目内容
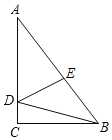
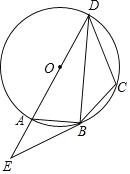
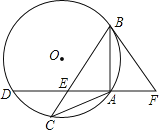
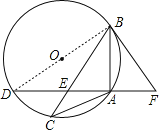
【题目】已知:如图,△ABC内接于⊙O,且AB=AC,点D在⊙O上,AD⊥AB于点A,AD与BC交于点E,F在DA的延长线上,且AF=AE.
(1)求证:BF与⊙O相切.
(2)若BF=5,cosC=![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)证明见解析;(2)⊙O半径为![]() .
.
【解析】
(1)连接BD,由于AB=AC,则∠ABC=∠C,由AF=AE,则∠EBA=∠FBA,从而得出∠ABD+∠FBA=90°,即OB⊥BF,则BF是⊙O切线;
(2) 因为∠C=∠D,得cos∠D=![]() =
=![]() ,设BD=4x,DF=5x,由BD2+BF2=DF2列出关于x的方程并求解,从而求出BD.
,设BD=4x,DF=5x,由BD2+BF2=DF2列出关于x的方程并求解,从而求出BD.
(1)连接BD,
∵AD⊥AB,
∴∠BAD=90°,
∴BD是直径,BD过圆心,
∵AB=AC,
∴∠ABC=∠C,
又∵∠C=∠D,
∴∠ABC=∠D,
∵AD⊥AB,
∴∠ABD+∠D=90°,
∵AF=AE,BA⊥EF,
∴AB是EF的垂直平分线,
∴BE=BF,
∴∠EBA=∠FBA,
∴∠ABF=∠D,
∵∠ABD+∠D=90°,
∴∠ABD+∠ABF=90°,
∴∠DBF=90°,
∴OB⊥BF,
又∵OB是⊙O的半径,
∴BF是⊙O切线;
(2)∵∠C=∠D,
∴cos∠D=cos∠C=![]() ,
,
在Rt△BDF中,
cos∠D=![]() =
=![]() ,
,
∴设BD=4x,DF=5x,
又∵BD2+BF2=DF2,
∴(4x)2+52=(5x)2,
x=![]() ,
,
∵x>0
∴x=![]() ,
,
∴BD=4×![]() =
=![]() ,
,
∴OB=![]() BD=
BD=![]() ,
,
∴⊙O半径为![]() .
.

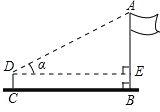
【题目】某校九年级四个数学活动小组参加测量操场旗杆高度的综合实践活动,如图是四个小组在不同位置测量后绘制的示意图,用测角仪测得旗杆顶端A的仰角记为α,CD为测角仪的高,测角仪CD的底部C处与旗杆的底部B处之间的距离记为CB,四个小组测量和计算数据如下表所示:
数据组别 | CD的长(m) | BC的长(m) | 仰角α | AB的长(m) |
第一组 | 1.59 | 13.2 | 32° | 9.8 |
第二组 | 1.58 | 13.4 | 31° | 9.6 |
第三组 | 1.57 | 14.1 | 30° | 9.7 |
第四组 | 1.56 | 15.2 | 28° |
(1)利用第四组学生测量的数据,求旗杆AB的高度(精确到0.1m);
(2)四组学生测量旗杆高度的平均值约为 m(精确到0.1m).
(参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)