Question

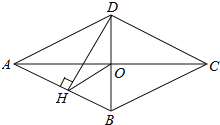
【题目】如图，四边形ABCD是菱形，对角线AC，BD相交于点O，DH⊥AB于点H，连接OH，∠CAD＝20°，则∠DHO的度数是（　　）

A.20°B.25°C.30°D.40°

Answer 1

【答案】A

【解析】

先根据菱形的性质得OD＝OB，AB∥CD，BD⊥AC，则利用DH⊥AB得到DH⊥CD，∠DHB＝90°，所以OH为Rt△DHB的斜边DB上的中线，得到OH＝OD＝OB，利用等腰三角形的性质得∠1＝∠DHO，然后利用等角的余角相等即可求出∠DHO的度数.

解：∵四边形ABCD是菱形，

∴OD＝OB，AB∥CD，BD⊥AC，

∵DH⊥AB，

∴DH⊥CD，∠DHB＝90°，

∴OH为Rt△DHB的斜边DB上的中线，

∴OH＝OD＝OB，

∴∠1＝∠DHO，

∵DH⊥CD，

∴∠1+∠2＝90°，

∵BD⊥AC，

∴∠2+∠DCO＝90°，

∴∠1＝∠DCO，

∴∠DHO＝∠DCA，

∵四边形ABCD是菱形，

∴DA＝DC，

∴∠CAD＝∠DCA＝20°，

∴∠DHO＝20°，

故选A．