题目内容
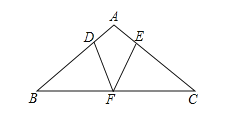
【题目】如图，是一块三角形材料，∠A＝30°，∠C＝90°，AB＝6．用这块材料剪出一个矩形DECF，点D，E，F分别在AB，BC，AC上，要使剪出的矩形DECF面积最大，点D应该选在何处？
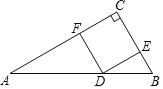
【答案】使剪出的矩形DECF面积最大，点D应该选在AB的中点．
【解析】
根据直角三角形的性质求出BC，根据勾股定理求出AC，根据矩形的面积公式列出函数解析式，根据二次函数的性质解答即可．
解：∵∠C＝90°，∠A＝30°，
∴BC＝
AB＝3，
由勾股定理得，AC＝
在Rt△ADF中，∠A＝30°，
∴AD＝2DF，AF＝
DF，
∴CF＝AC﹣AF＝
DF，
则矩形DECF面积＝DF×（DF）
＝﹣DF2+3DF=
当DF＝
时，剪出的矩形DECF面积最大，
则AD＝2DF＝3，
∴使剪出的矩形DECF面积最大，点D应该选在AB的中点．
练习册系列答案
相关题目
【题目】某农科所在相同条件下做某种作物种子发芽率的试验，结果如表所示：
种子个数n | 1000 | 1500 | 2500 | 4000 | 8000 | 15000 | 20000 | 30000 |
发芽种子个数m | 899 | 1365 | 2245 | 3644 | 7272 | 13680 | 18160 | 27300 |
发芽种子频率 | 0.899 | 0.910 | 0.898 | 0.911 | 0.909 | 0.912 | 0.908 | 0.910 |
则该作物种子发芽的概率约为_____________．（保留一位小数）
