题目内容
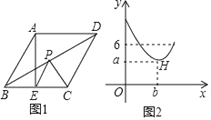
【题目】已知:如图,在平行四边形中,点E在BC边上,连接AE.O为AE中点,连接BO并延长交AD于F.
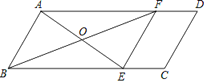
(1)求证:△AOF≌△BOE,
(2)判断当AE平分∠BAD时,四边形ABEF是什么特殊四边形,并证明你的结论.
【答案】(1)求证:见解析;(2)四边形ABEF是菱形,见解析.
【解析】
(1)先利用平行四边形的性质得AD∥BC,则∠AFB=∠CBF,然后根据“AAS”可判断△AOF≌△BOE;
(2)利用△AOF≌△BOE得到FO=BO,则可根据对角线互相平分可判定四边形ABEF是平行四边形,根据AE平分∠BAD,得∠BAE=∠FAE,又∠FAE=∠AEB,得∠BAE=∠AEB,AB=BE,有一组对边相等的平行四边形是菱形,得四边形ABEF是菱形.
(1)∵O为AE中点,
∴AO=EO,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠AFB=∠CBF,
在△AOF和△BOE中
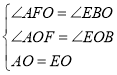 ,
,
∴△AOF≌△BOE;
(2)四边形ABEF是菱形,理由如下:
∵△AOF≌△BOE,
∴FO=BO,
而AO=EO,
∴四边形ABEF是平行四边形,
∵AE平分∠BAD,
∴∠BAE=∠FAE,
∵∠FAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴四边形ABEF是菱形.

【题目】下表是2019年三月份某居民小区随机抽取20户居民的用水情况:
用水量/吨 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
户数 | 2 | 4 | m | 4 | 3 | 0 | 1 |
(1)求出m= ,补充画出这20户家庭三月份用电量的条形统计图;
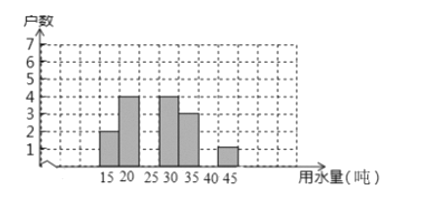
(2)据上表中有关信息,计算或找出下表中的统计量,并将结果填入表中:
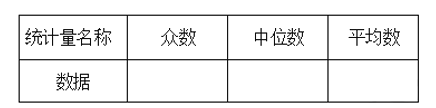
(3)为了倡导“节约用水,绿色环保”的意识,台州市自来水公司实行“梯级用水、分类计费”,价格表如下:

如果该小区有500户家庭,根据以上数据,请估算该小区三月份有多少户家庭在ⅠI级标准?并估算这些级用水户的总水费是多少?