题目内容
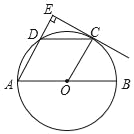
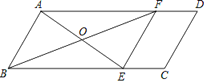
【题目】如图,港口B位于港口A的南偏西45°方向,灯塔C恰好在AB的中点处.一艘海轮位于港口A的正南方向,港口B的南偏东45°方向的D处,它沿正北方向航行18.5 km到达E处,此时测得灯塔C在E的南偏西70°方向上,求E处距离港口A有多远?
(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
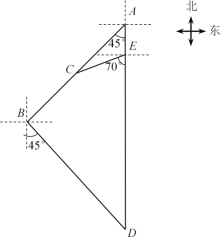
【答案】3.5 km.
【解析】
过点B作BM⊥AD,垂足为M,过点C作CN⊥AD,垂足为N,设CN=x km,在Rt△ACN中,利用∠A的正切值可得AN=x,在Rt△ECN中,利用∠CEN的正切值可得EN=![]() ,根据平行线分线段成比例性质可得
,根据平行线分线段成比例性质可得![]() ,可得BM=2x,AN=MN,在Rt△BMD中,利用∠MDB的正切值可得DM=2x,根据DE-DM-EN=MN列方程即可求出x的值,进而可得AE的长.
,可得BM=2x,AN=MN,在Rt△BMD中,利用∠MDB的正切值可得DM=2x,根据DE-DM-EN=MN列方程即可求出x的值,进而可得AE的长.
如图,过点B作BM⊥AD,垂足为M,过点C作CN⊥AD,垂足为N.
设CN=x km.
在Rt△ACN中,∠A=45°,
∴tan45°=![]() ,
,
∴AN=![]() =
=![]() =x,
=x,
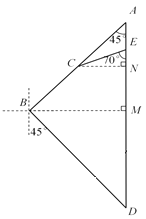
在Rt△ECN中,∠CEN=70°,
∵tan70°=![]() ,
,
∴EN=![]() =
=![]() .
.
∵CN⊥AD,BM⊥AD,
∴∠ANC=∠AMB=90°.
∴CN∥BM.
∴![]() .
.
又∵C为AB中点,
∴AB=2AC,AC=BC.
∴BM=2CN=2x,AN=MN.
由题可知,∠MDB=45°.
在Rt△BMD中,∠MDB=45°,
∵tan45°=![]() ,
,
∴DM=![]() =
=![]() =2x.
=2x.
∴18.5-2x-![]() =x
=x
∴x=![]() ≈5.5.
≈5.5.
∴AE=AN-EN=5.5-![]() =3.5.
=3.5.
因此,E处距离港口A大约3.5km.

练习册系列答案
相关题目