题目内容
【题目】M、N两同学在做一种游戏，规定每人随机伸出一只手中的1根至5根手指，两人伸出的手指的和若为2，3，4，8，9，10，则M胜；若和为5，6，7，则N胜.
(1)用画树状图法分别求M、N两人获胜的概率；
(2)上面的游戏公平吗？若不公平，你能否设计一个方案使游戏绝对公平？若能，写出方案；若不能，说明理由.
【答案】(1)M获胜的概率是
，N获胜的概率是
；(2)游戏不公平，能设计一个方案使游戏绝对公平，方案见解析.
【解析】
(1)根据题意题意画出树状图得出所有等情况数和和为2，3，4，8，9，10的情况数以及和为5，6，7的情况数，然后根据概率公式即可得出答案；
(2)游戏是否公平，关键要看游戏双方取胜的机会是否相等，即判断双方取胜的概率是否相等，或转化为在总情况明确的情况下，判断双方取胜所包含的情况数目是否相等.
解：(1)根据题意画树状图如下：
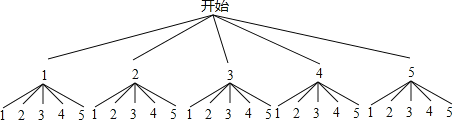
由图知，和共有25种等情况数，其中和为2，3，4，8，9，10的共出现了12次，和为5，6，7出现了13次，
所以M获胜的概率是，N获胜的概率是；
(2)这个游戏不公平，因为M获胜的概率是，N获胜的概率是，所以N获胜的概率大，
可设计如下的方案使游戏绝对公平，规定两人随机伸出5根手指中的任何几根，和为2，3，4，则M胜，和为8，9，10，则N胜.
练习册系列答案
相关题目
