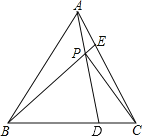
题目内容
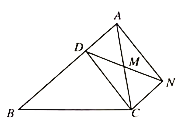
【题目】如图,正方形ABCD中,P为AD上一点,BP⊥PE交BC的延长线于点E,若AB=6,AP=4,则CE的长为_____.
【答案】7
【解析】
利用同角的余角相等可得出∠ABP=∠DPF,结合∠A=∠D可得出△APB∽△DFP,利用相似三角形的性质可求出DF的长,进而可得出CF的长,由∠PFD=∠EFC,∠D=∠ECF可得出△PFD∽△EFC,再利用相似三角形的性质可求出CE的长.
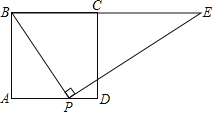
∵四边形ABCD为正方形,
∴∠A=∠D=∠ECF=90°,AB=AD=CD=6,
∴DP=AD﹣AP=2.
∵BP⊥PE,
∴∠BPE=90°,
∴∠APB+∠DPF=90°.
∵∠APB+∠ABP=90°,
∴∠ABP=∠DPF.
又∵∠A=∠D,
∴△APB∽△DFP,
∴![]() ,即
,即![]() ,
,
∴DF=![]() ,
,
∴CF=![]() .
.
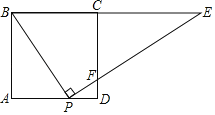
∵∠PFD=∠EFC,∠D=∠ECF,
∴△PFD∽△EFC,
∴![]() =
=![]() ,即
,即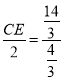 ,
,
∴CE=7.
故答案为:7.

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
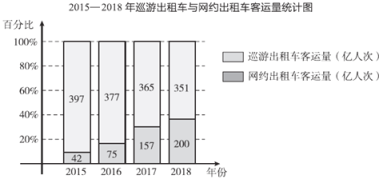
波波熊暑假作业江西人民出版社系列答案【题目】黄山毛峰是中国十大名茶之一 ,产于安徽省黄山(徽州)一带,也称徽茶.有诗日:“未见黄山面,十里闻茶香”.某茶庄以![]() 元
元![]() 的价格收购一批毛峰,物价部门规定销售单价不低于成本且不得超过成本的
的价格收购一批毛峰,物价部门规定销售单价不低于成本且不得超过成本的![]() 倍,经试销过发现,日销量
倍,经试销过发现,日销量![]() 与销售单价
与销售单价![]() 的对应关系如下表:且
的对应关系如下表:且![]() 与
与![]() 满足初中所学某种函数关系.
满足初中所学某种函数关系.
|
|
|
|
| ··· |
|
|
|
|
| ··· |
(1)根据表格,求出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)在销售过程中,每日还需支付其他费用![]() 元,当销售单价为多少时,该茶庄日利润最大?最大利润是多少元?
元,当销售单价为多少时,该茶庄日利润最大?最大利润是多少元?
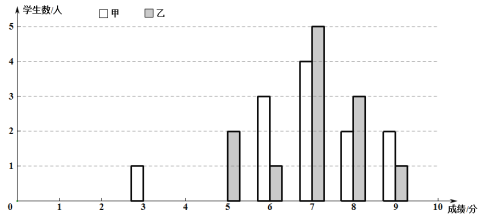
【题目】某校为调查“停课不停学”期间九年级学生平均每天上网课时长,随机抽取了![]() 名九年级学生做网络问卷调查.共四个选项:
名九年级学生做网络问卷调查.共四个选项:![]() 小时以下)、
小时以下)、![]() 小时)、
小时)、![]() 小时),
小时), ![]() 小时以上),每人只能选一
小时以上),每人只能选一
项.并将调查结果绘制成如下不完整的统计表和统计图.
被调查学生平均每天上网课时间统计表
时长 | 所占百分比 |
|
|
|
|
|
|
|
|
合计 |
|
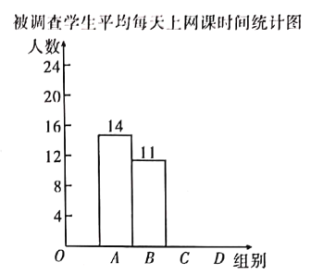
根据以上信息,解答下列问题:
![]() ,
,![]() ,
,
![]() 补全条形统计图;
补全条形统计图;
![]() 该校有九年级学生
该校有九年级学生![]() 名,请你估计仝校九年级学生平均每天上网课时长在
名,请你估计仝校九年级学生平均每天上网课时长在![]() 小时及以上的共多少名;
小时及以上的共多少名;
![]() 在被调查的对象中,平均每天观看时长超过
在被调查的对象中,平均每天观看时长超过![]() 小时的,有
小时的,有![]() 名来自九
名来自九![]() 班,
班,![]() 名来自九
名来自九![]() 班,其余都来自九
班,其余都来自九![]() 班,现教导处准备从
班,现教导处准备从![]() 选项中任选两名学生进行电话访谈,请用列表法或画树状图的方法求所抽取的
选项中任选两名学生进行电话访谈,请用列表法或画树状图的方法求所抽取的![]() 名学生恰好来自同一个班级的概率.
名学生恰好来自同一个班级的概率.