题目内容
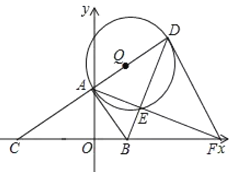
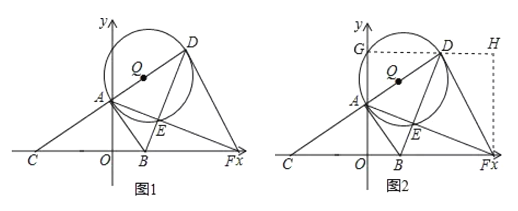
【题目】如图,在平面直角坐标系![]() 中,已知点
中,已知点![]() ,点B是
,点B是![]() 轴正半轴上一点,连接
轴正半轴上一点,连接![]() ,过点A作
,过点A作![]() ,交
,交![]() 轴于点C,点D是点C关于点A的对称点,连接
轴于点C,点D是点C关于点A的对称点,连接![]() ,以
,以![]() 为直径作
为直径作![]() 交
交![]() 于点E,连接AE并延长交
于点E,连接AE并延长交![]() 轴于点F,连接DF.
轴于点F,连接DF.
(1)求线段AE的长;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若![]() 与
与![]() 相似,求
相似,求![]() 的值.
的值.
【答案】(1)4;(2)![]() ;(3)
;(3)![]() 或8
或8
【解析】
(1)由AD是圆Q的直径可得:∠AEB=∠AED=90°,再由BA垂直平分CD可得:BC=BD,然后证明![]() ,即可解答;
,即可解答;
(2)设![]() ,则
,则![]() ,根据勾股定理可得:x=3,再证明△BFA∽△AFC,最后运用正切的定义即可解答;
,根据勾股定理可得:x=3,再证明△BFA∽△AFC,最后运用正切的定义即可解答;
(3)需要分![]() 和
和![]() 两种情况解答即可.
两种情况解答即可.
(1)∵AB是![]() 的直径
的直径
![]()
![]()
∵BA垂直平分CD,
![]()
![]()
![]()
![]()
(2)设![]() ,则
,则![]()
在![]() 中,由
中,由![]() 得
得![]() ,解得:
,解得:![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
设![]() ,则
,则![]()
在![]() 中,
中, ![]()
![]()
解得![]()
∴![]() =
=
(3)①如图1,当![]() 时,有
时,有![]()
![]()
BD垂直平分AF
![]()
②如图2,设![]() 交
交![]() 轴于点
轴于点![]() ,连接DG,作
,连接DG,作![]() 于H
于H
当![]() 时,有
时,有![]()
![]()
![]()
综上所述,![]() 或8;
或8;

练习册系列答案
相关题目
【题目】某校为调查“停课不停学”期间九年级学生平均每天上网课时长,随机抽取了![]() 名九年级学生做网络问卷调查.共四个选项:
名九年级学生做网络问卷调查.共四个选项:![]() 小时以下)、
小时以下)、![]() 小时)、
小时)、![]() 小时),
小时), ![]() 小时以上),每人只能选一
小时以上),每人只能选一
项.并将调查结果绘制成如下不完整的统计表和统计图.
被调查学生平均每天上网课时间统计表
时长 | 所占百分比 |
|
|
|
|
|
|
|
|
合计 |
|
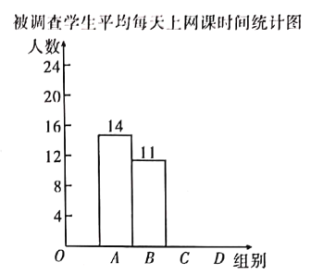
根据以上信息,解答下列问题:
![]() ,
,![]() ,
,
![]() 补全条形统计图;
补全条形统计图;
![]() 该校有九年级学生
该校有九年级学生![]() 名,请你估计仝校九年级学生平均每天上网课时长在
名,请你估计仝校九年级学生平均每天上网课时长在![]() 小时及以上的共多少名;
小时及以上的共多少名;
![]() 在被调查的对象中,平均每天观看时长超过
在被调查的对象中,平均每天观看时长超过![]() 小时的,有
小时的,有![]() 名来自九
名来自九![]() 班,
班,![]() 名来自九
名来自九![]() 班,其余都来自九
班,其余都来自九![]() 班,现教导处准备从
班,现教导处准备从![]() 选项中任选两名学生进行电话访谈,请用列表法或画树状图的方法求所抽取的
选项中任选两名学生进行电话访谈,请用列表法或画树状图的方法求所抽取的![]() 名学生恰好来自同一个班级的概率.
名学生恰好来自同一个班级的概率.