Question

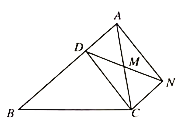
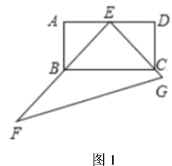
【题目】如图1，边长为4的正方形与边长为的正方形的顶点重合，点在对角线上．

问题发现

（1）如图1，与的数量关系为______．

类比探究

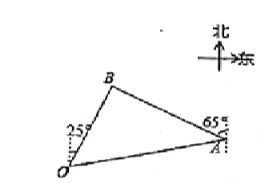
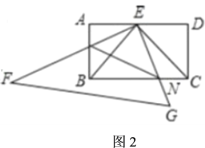
（2）如图2，将正方形绕点旋转度（）．请问（1）中的结论还成立吗？若不成立，请说明理由．

拓展延伸

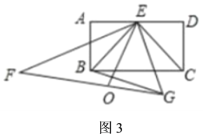
（3）若为的中点，在正方形的旋转过程中，当点，，在一条直线上时，线段的长度为______．

Answer 1

【答案】（1）；（2）成立，见解析；（3）或

【解析】

问题发现：证出AB∥EF，由平行线分线段成比例定理得出，即可得出结论；

类比探究：证明△ACE∽△BCF，得出，即可的结论；

拓展延伸：分两种情况，连接CE交GF于H，由正方形的性质得出AB=BC=4，，，GH=HF=HE=HC，得出，，，由勾股定理求出，即可得出答案．

[问题发现]

解：，理由如下：

∵四边形ABCD和四边形CFEG是正方形，

∴∠B=∠CFE=90°，∠FCE=∠BCA=45°，CE=CF，CE⊥GF，

∴AB∥EF，

∴，

；

故答案为：；

[类比探究]

解：上述结论还成立，理由如下：

连接CE，如图2所示：

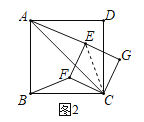
∵∠FCE=∠BCA=45°，

∴∠BCF=∠ACE=45°-∠ACF，

在Rt△CEG和Rt△CBA中，

，

，

∴△ACE∽△BCF，

，

；

[拓展延伸]

解：分两种情况：

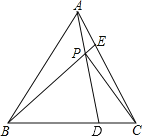
①如图3所示：

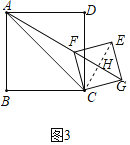
连接CE交GF于H，

∵四边形ABCD和四边形CFEG是正方形，

∴AB=BC=4，AC=AB=4，GF=CE=CF，HF=HE=HC，

∵点F为BC的中点，

∴CF=BC=2，GF=CE=2，GH=HF=HE=HC=，

∴，

∴；

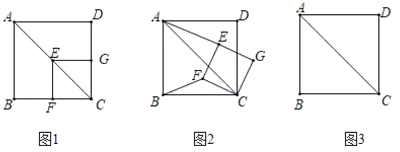
②如图4所示：连接CE交GF于H，

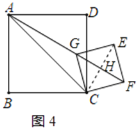
同①得：GH=HF=HE=HC=，

∴，

∴；

故答案为：或．