Question

【题目】如图，一抛物线经过点A（﹣2，0），点B（0，4）和点C（4，0），该抛物线的顶点为D．

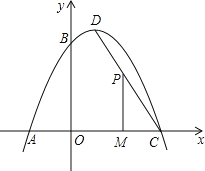
（1）求该抛物线的函数关系式及顶点D坐标．

（2）如图，若P为线段CD上的一个动点，过点P作PM⊥x轴于点M，求四边形PMAB的面积的最大值和此时点P的坐标．

（3）过抛物线顶点D，作DE⊥x轴于E点，F（m，0）是x轴上一动点，若以BF为直径的圆与线段DE有公共点，求m的取值范围．

Answer 1

【答案】（1）y=﹣+x+4．D的坐标为（1，）．（2）点P的坐标为（，1）．（3）m的取值范围为﹣3≤m≤．

【解析】

试题分析：（1）设抛物线的解析式为y=a（x+2）（x﹣4），把（0，4）代入求得a=﹣，从而可求得抛物线的解析式，然后依据配方法可求得抛物线的顶点坐标；

（2）依据待定系数法可求得直线CD的解析式为y═﹣x+6．设点P的坐标为（a，﹣a+6），则PM=﹣a+6，然后根据SPMAB=S△AOB+SPMOB可求得四边形PMAB的面积与a的函数关系式，最后依据配方法可求得四边形的最大面积以及点P的坐标；

（3）先依据勾股定理可求得BF2=m2+16，即r=，当如图1所示；当圆G与DE相切时，GH=r=（1﹣）得到（1﹣）2=+4，可求得m=﹣3，

如图2所示：点F在点E右侧且该圆经过点D时．由两点间的距离公式可知DG2=r2=（）2+（）2可知+4=（﹣1）2+（）2，从而可解得m=，故此可求得m的取值范围是﹣3≤m≤．

解：（1）由题意设y=a（x+2）（x﹣4），把（0，4）代入得：﹣8a=4，

解得：a=﹣．

∴该抛物线的解析式为y=﹣（x+2）（x﹣4）．

整理得：y=﹣+x+4．

∵y=﹣+x+4=﹣（x﹣1）2+，

∴顶点D的坐标为（1，）．

（2）设直线CD的函数关系式为y=kx+b，

∵把C（4，0），D（1，）代入得k=﹣，b=6，

∴直线CD的函数关系式为y=﹣x+6．

设点P的坐标为（a，﹣a+6），

∵SPMAB=S△AOB+SPMOB，

∴四边形PMAB的面积=×2×4+×（﹣a+6+4）×a=﹣a2+5a+4=﹣（a﹣）2+．

∴当a=时，四边形PMAB的面积最大，最大面积为．

∴点P的坐标为（，1）．

（3）∵点F的坐标为（m，0），点B的坐标为（0，4）

∴圆心G的坐标为（，2）．

在Rt△BOF中由勾股定理可知：BF2=OB2+OF2=16+m2=4r2．

①如图1所示；当圆G与DE相切时．

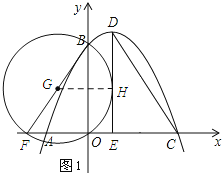
∵DE与圆G相切，

∴r=1﹣．

r2=+4．

∴（1﹣）2=+4．

解得：m=﹣3．

②如图2所示：点F在点E右侧且该圆经过点D时．

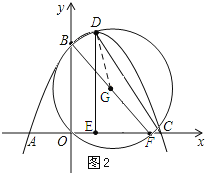
∵点D在圆G上，

∴DG2=（）2+（）2=r2．

∴+4=（﹣1）2+（）2．

解得：m=．

综上所述，m的取值范围为﹣3≤m≤．