题目内容
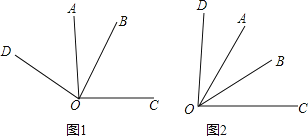
【题目】已知∠AOC=∠BOD=α(0°<α<180°)
(1)如图1,若α=90°
①写出图中一组相等的角(除直角外) ,理由是
②试猜想∠COD和∠AOB在数量上是相等、互余、还是互补的关系,并说明理由;
(2)如图2,∠COD+∠AOB和∠AOC满足的等量关系是 ;当α= °,∠COD和∠AOB互余.
【答案】(1)AOD=∠BOC,同角的余角相等;(2)互补,45.
【解析】
试题分析:(1)①根据同角的余角相等解答;
②表示出∠AOD,再求出∠COD,然后整理即可得解;
(2)根据(1)的求解思路解答即可.
解:(1)①∵∠AOC=∠BOD=90°,
∴∠AOD+∠AOB=∠BOC+∠AOB=90°,
∴∠AOD=∠BOC;
②∵∠AOD=∠BOD﹣∠AOB=90°﹣∠AOB,
∴∠COD=∠AOD+∠AOC=90°﹣∠AOB+90°,
∴∠AOB+∠COD=180°,
∴∠COD和∠AOB互补;
(2)由(1)可知∠COD+∠AOB=∠BOD+∠AOC=α+α=2α,
所以,∠COD+∠AOB=2∠AOC,
若∠COD和∠AOB互余,则2∠AOC=90°,
所以,∠AOC=45°,
即α=45°.
故答案为:(1)AOD=∠BOC,同角的余角相等;(2)互补,45.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目