题目内容
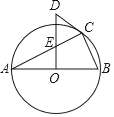
【题目】如图，△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线交BC于点D，垂足为E，若DE=2cm，则BD的长为_______.
【答案】8cm.
【解析】
根据等腰三角形两底角相等求出∠C=30°，再根据直角三角形30°角所对的直角边等于斜边的一半可得CD=2DE=4cm，然后再根据垂直平分线的性质得到AD=CD=4cm，∠CAD=∠C=30°，即可得解．
解：∵AB=AC，∠BAC=120°，
∴∠B=∠C=30°，
∵DE是AC的垂直平分线，
∴AD=CD,∠CAD=∠C=30°，∠CED=90°.
∴AD=CD=2DE=4cm.
∵∠BAC=120°，
∴∠BAD=∠BAC-∠CAD=90°.
∴BD=2AD=8cm.
故答案为8cm.
练习册系列答案
相关题目
【题目】小颖和小红两位同学在学习“概率”时，做掷骰子（质地均匀的正方体）实验．
他们在一次实验中共掷骰子
次，试验的结果如下：
朝上的点数 |
|
|
|
|
|
|
出现的次数 |
|
|
|
|
|
|
①填空：此次实验中“
点朝上”的频率为________；
②小红说：“根据实验，出现点朝上的概率最大．”她的说法正确吗？为什么？
小颖和小红在实验中如果各掷一枚骰子，那么两枚骰子朝上的点数之和为多少时的概率最大？试用列表或画树状图的方法加以说明，并求出其最大概率．
