Question

【题目】如图，矩形ABCD中，AB＞AD，把矩形沿对角线AC所在直线折叠，使点B落在点E处，AE交CD于F，连接DE．

（1）求证：△ADE≌△CED

（2）若AD＝4，AB＝8，求△ACF的面积．

Answer 1

【答案】（1）见解析；（2）10．

【解析】

（1）根据矩形的性质可得出AD=BC、AB=CD，结合折叠的性质可得出AD=CE、AE=CD，进而即可证出△ADE≌△CED（SSS）；
（2）由矩形的性质得出AB∥CD，CD=AB=8，∠ADC=90°，得出∠ACD=∠BAC，由折叠的性质得∠BAC=∠EAC，得出∠ACD=∠EAC，证出AF=CF，设AF=CF=x，则DF=CD-CF=8-x，在Rt△ADF中，由勾股定理得出方程，得出CF=5，由三角形面积公式即可得出答案．

（1）证明：∵四边形ABCD是矩形，

∴AD＝BC，AB＝CD．

由折叠的性质可得：BC＝CE，AB＝AE，

∴AD＝CE，AE＝CD．

在△ADE和△CED中，，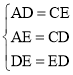

∴△ADE≌△CED（SSS）．

（2）解：∵四边形ABCD是矩形，

∴AB∥CD，CD＝AB＝8，∠ADC＝90°，

∴∠ACD＝∠BAC，

由折叠的性质得：∠BAC＝∠EAC，

∴∠ACD＝∠EAC，

∴AF＝CF，

设AF＝CF＝x，则DF＝CD﹣CF＝8﹣x，

在Rt△ADF中，由勾股定理得：42+（8﹣x）2＝x2，

解得：x＝5，

∴CF＝5，

∴△ACF的面积＝CF×AD＝×5×4＝10．