��Ŀ����
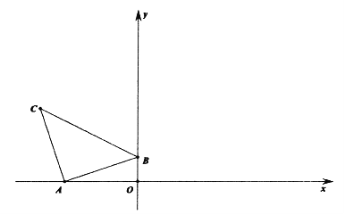
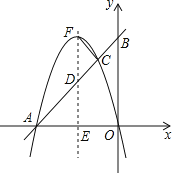
����Ŀ����ͼ����ֱ������ϵ�У�O������ԭ�㣬ֱ��AB��x���ڵ�A����4��0������y���ڵ�B��������y=ax2+2ax+3��a��0������A��B���㣮P���߶�AO�ϵ�һ���㣬����P��PC��x�ύֱ��AB�ڵ�C�����������ڵ�D��
��1����a��AB�ij���
��2������PB����tan��ABP=![]() �����P�����꣮
�����P�����꣮
��3������BD����BDΪ����������BDEF���Ƿ���ڵ�Pʹ��Eǡ�����������ߵĶԳ����ϣ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
��4������OC����S��BDC��S��OBC=1��2�����߶�BD�Ƶ�D��˳ʱ�뷽����ת���õ�DB����������ת�Ĺ����У�����A��B��ֱ��DB���ľ�������ʱ����ֱ��д����B�������꣮
���𰸡���1��a=��![]() ��AB�ij�Ϊ5����2����P�����꣨��1.5��0������3��Eǡ�����������ߵĶԳ����������������P������Ϊ��
��AB�ij�Ϊ5����2����P�����꣨��1.5��0������3��Eǡ�����������ߵĶԳ����������������P������Ϊ��![]() ��0��������4��0������4������A��B��ֱ��DB���ľ�������ʱ��B��������Ϊ����
��0��������4��0������4������A��B��ֱ��DB���ľ�������ʱ��B��������Ϊ����![]() ����
����
��������
��1���ѵ�A����4��0������������y=ax2+2ax+3���̼��������
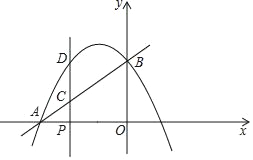
��2����ͼ������BP����AH��PB��H�����P������Ϊ��x��0������OP=��x��AP=4+x��BP=![]() ����֤����APH�ס�BPO�������������εĶ�Ӧ�߳ɱ������з��̲���⼴�ɵõ�������
����֤����APH�ס�BPO�������������εĶ�Ӧ�߳ɱ������з��̲���⼴�ɵõ�������
��3����ͼ��ʾ��������DBFE��E���������ߵĶԳ�������֤��Rt��BHD��Rt��END��AAS������EN=BH���������
��4��������BDC����OBC�ǵȸ߲��ȵ����������������CD![]() OB
OB![]() �����D�����꣨m��
�����D�����꣨m��![]() �����ѵ�D�����������κ�������y
�����ѵ�D�����������κ�������y![]() x2
x2![]() x+3�������D��������D����2��3������B��0��3����BD��x������Rt��B'MD����B'D=BD=2��tan��B'DP
x+3�������D��������D����2��3������B��0��3����BD��x������Rt��B'MD����B'D=BD=2��tan��B'DP![]() ������B'M
������B'M![]() ��DM
��DM![]() �����������
�����������
��1���ѵ�A����4��0������������y=ax2+2ax+3���̽����a![]() �����κ����ı���ʽΪ��y
�����κ����ı���ʽΪ��y![]() x2
x2![]() x+3����B������0��3����
x+3����B������0��3����
��OA=4��OB=3���ɹ��ɶ�������AB=5������κ�������ʽΪ��y![]() x2
x2![]() x+3���Գ���Ϊx=��1��
x+3���Գ���Ϊx=��1��
����a![]() ��AB�ij�Ϊ5��
��AB�ij�Ϊ5��
��2����ͼ������BP����AH��PB��H����Rt��ABH����AB=5��tan��ABP![]() ���ɵ���AH
���ɵ���AH![]() ��BH=2
��BH=2![]() �����P��������x��0������OP=��x��AP=4+x��BP=
�����P��������x��0������OP=��x��AP=4+x��BP=![]() =
=![]() ��
��
�ߡ�APH=��BPO����AHP=��POB=90�㣬���APH�ס�BPO����![]() ����
����![]() ����������4x2+72x+99=0���ࣨ2x+3����2x+33��=0�������x=��1.5����x=��16.5����ȥ��������P������Ϊ����1.5��0����
����������4x2+72x+99=0���ࣨ2x+3����2x+33��=0�������x=��1.5����x=��16.5����ȥ��������P������Ϊ����1.5��0����
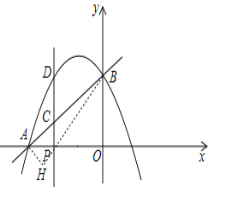
��3����ͼ��ʾ��������DBFE��E���������ߵĶԳ���������E����EN��PD����DH��y������Rt��BHD��Rt��END��AAS������EN=BH����P������Ϊ��a��0������D��E�������ֱ�Ϊ��a��![]() a2
a2![]() a+3��������1��y����BH=3����
a+3��������1��y����BH=3����![]() a2
a2![]() a+3��=EN=��1��a�������x
a+3��=EN=��1��a�������x![]() ��x=��4��
��x=��4��
����Eǡ�����������ߵĶԳ����������������P������Ϊ��![]() ��0��������4��0����
��0��������4��0����

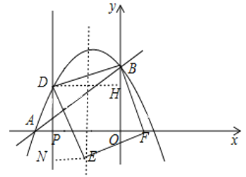
��4����BD��ת����ͼDB'��λ��ʱ����A��B��ֱ��DB'�ľ�����������ʱAB��B'D������B'��PD��x������������B'M��DP��B'N��x������A��B��������ɵ�AB��ֱ�߷���Ϊ��y![]() x+3����tan��BAO
x+3����tan��BAO![]() ����P��������m��0������C��m��
����P��������m��0������C��m��![]() m+3����
m+3����
�ߡ�BDC����OBC�ǵȸ߲��ȵ���������������1��2��S��BDC��S��OBC=1��2����CD![]() OB
OB![]() ����D��y����=C��y����
����D��y����=C��y����![]() ������D��m��
������D��m��![]() �����ѵ�D�����꣨m��
�����ѵ�D�����꣨m��![]() ��������κ�������y
��������������y![]() x2
x2![]() x+3�������m=��2����mֵ��������D������Ϊ��D����2��3����P����2��0����
x+3�������m=��2����mֵ��������D������Ϊ��D����2��3����P����2��0����
��B��0��3����BD��x������BD��DC��
��BD��DC��AB��B'D��DP��AP�����B'DP=��BAO����tan��B'DP=tan��BAO![]() ����Rt��B'MD����B'D=BD=2��tan��B'DP
����Rt��B'MD����B'D=BD=2��tan��B'DP![]() ������B'M
������B'M![]() ��DM
��DM![]() ������B'�ĺ�����Ϊ=xP��B'M=��2
������B'�ĺ�����Ϊ=xP��B'M=��2![]() ��B'��������Ϊ=yD��DM=3
��B'��������Ϊ=yD��DM=3![]() ��
��
��������A��B��ֱ��DB'�ľ�������ʱ��B'������Ϊ��![]() ����
����

 ������ÿ�ʱ�Ż���ҵϵ�д�
������ÿ�ʱ�Ż���ҵϵ�д�