题目内容
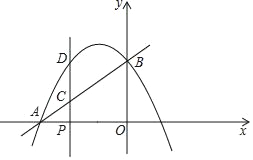
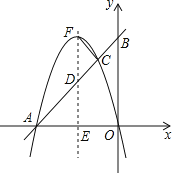
【题目】如图，二次函数y=ax2+bx（a＜0）的图象过坐标原点O，与x轴的负半轴交于点A，过A点的直线与y轴交于B，与二次函数的图象交于另一点C，且C点的横坐标为﹣1，AC：BC=3：1．
（1）求点A的坐标；
（2）设二次函数图象的顶点为F，其对称轴与直线AB及x轴分别交于点D和点E，若△FCD与△AED相似，求此二次函数的关系式．
【答案】（1）（﹣4，0）；（2）y=﹣x2﹣4x．
【解析】
试题（1）过点C作CM∥OA交y轴于M，则△BCM∽△BAO，根据相似三角形对应边成比例得出
，即OA=4CM=4，由此得出点A的坐标为（﹣4，0）.
（2）先将A（﹣4，0）代入y=ax2+bx，化简得出b=4a，即y=ax2+4ax，则顶点F（﹣2，﹣4a），设直线AB的解析式为y=kx+n，将A（﹣4，0）代入，化简得n=4k，即直线AB的解析式为y=kx+4k，则B点（0，4k），D（﹣2，2k），C（﹣1，3k）．由C（﹣1，3k）在抛物线y=ax2+4ax上，得出3k=a﹣4a，化简得到k=﹣a．再由△FCD与直角△AED相似，则△FCD是直角三角形，又∠FDC=∠ADE＜90°，∠CFD＜90°，得出∠FCD=90°，△FCD∽△AED．再根据两点之间的距离公式得出FC2=CD2=1+a2，得出△FCD是等腰直角三角形，则△AED也是等腰直角三角形，所以∠DAE=45°，由三角形内角和定理求出∠OBA=45°，那么OB=OA=4，即4k=4，求出k=1，a=﹣1，进而得到此二次函数的关系式为y=﹣x2﹣4x．
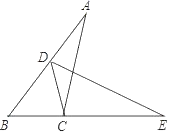
试题解析：解：（1）如答图，过点C作CM∥OA交y轴于M．
∵AC：BC=3：1，∴
．
∵CM∥OA，∴△BCM∽△BAO.∴.
∵C点的横坐标为﹣1，∴CM=1.∴OA=4CM=4.
∴点A的坐标为（﹣4，0）.
（2）∵二次函数y=ax2+bx（a＜0）的图象过A点（﹣4，0），
∴16a﹣4b=0.∴b=4a.
∴y=ax2+4ax，对称轴为直线x=﹣2，F点坐标为（﹣2，﹣4a）．
设直线AB的解析式为y=kx+n，将A（﹣4，0）代入，得﹣4k+n=0，∴n=4k.
∴直线AB的解析式为y=kx+4k.
∴B点坐标为（0，4k），D点坐标为（﹣2，2k），C点坐标为（﹣1，3k）．
∵C（﹣1，3k）在抛物线y=ax2+4ax上，∴3k=a﹣4a，∴k=﹣a．
∵△AED中，∠AED=90°，
∴若△FCD与△AED相似，则△FCD是直角三角形.
∵∠FDC=∠ADE＜90°，∠CFD＜90°，∴∠FCD=90°.
∴△FCD∽△AED．
∵F（﹣2，﹣4a），C（﹣1，3k），D（﹣2，2k），k=﹣a，
∴FC2=（﹣1+2）2+（3k+4a）2=1+a2，CD2=（﹣2+1）2+（2k﹣3k）2=1+a2.
∴FC=CD.∴△FCD是等腰直角三角形.∴△AED是等腰直角三角形.
∴∠DAE=45°.∴∠OBA=45°.∴OB=OA=4.
∴4k=4.∴k=1.∴a=﹣1.
∴此二次函数的关系式为y=﹣x2﹣4x．
