题目内容
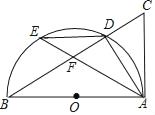
【题目】如图,在Rt△ABC中,∠BAC=90°,以边AB为直径作⊙O,交斜边BC于D,E在弧![]() 上,连接AE、ED、DA,连接AE、ED、DA.
上,连接AE、ED、DA,连接AE、ED、DA.
(1)求证:∠DAC=∠AED;
(2)若点E是![]() 的中点,AE与BC交于点F,当BD=5,CD=4时,求DF的长.
的中点,AE与BC交于点F,当BD=5,CD=4时,求DF的长.
【答案】(1)详见解析;(2)DF=2.
【解析】
(1)根据圆周角定理得到AD⊥BC,根据余角的性质和圆周角定理即可得到结论;
(2)根据等腰三角形的性质得到CA=CF,根据相似三角形的性质即可得到结论.
(1)证明:∵AB是⊙O的直径,
∴AD⊥BC,
∵∠BAC=90°,
∴∠CAD+∠BAD=∠BAD+∠B=90°,
∴∠CAD=∠B,
∵∠E=∠ABD,
∴∠DAC=∠AED;
(2)∵点E是![]() 的中点,
的中点,
∴∠BAE=∠EAD,
∵∠CFA=∠ABC+∠BAE,∠CAE=∠CDA+∠EAD,
∴∠CFA=∠CAE,
∴CA=CF,
∵∠BAC=∠ADB=90°,
∴∠ACD=∠BCA,
∴△ADC∽△BAC,
∴![]() ,
,
即AC2=BC×CD=(5+4)×4=36,
解得AC=6,
∴CA=CF=6,
∴DF=CA﹣CD=2.

练习册系列答案
相关题目