题目内容
【题目】已知正方形![]() 的对角线
的对角线![]() ,
,![]() 相交于点
相交于点![]() .
.
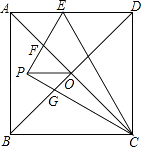
(1)如图1,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,
上的点,![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() .若
.若![]() ,求证:
,求证:![]() ;
;
(2)如图2,![]() 是
是![]() 上的点,过点
上的点,过点![]() 作
作![]() ,交线段
,交线段![]() 于点
于点![]() ,连结
,连结![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .若
.若![]() ,
,
①求证:![]() ;
;
②当![]() 时,求
时,求![]() 的长.
的长.

【答案】(1)证明见解析(2)①证明见解析②![]()
【解析】
试题分析:(1)根据正方形的性质,可根据三角形全等的判定(ASA)与性质求证即可;
(2)①同(1)中,利用上面的结论,根据SAS可证的结论;
②设CH=x,然后根据正方形的性质和相似三角形的判定与性质可得![]() ,然后列方程求解即可.
,然后列方程求解即可.
试题解析:(1)证明:∵四边形ABCD是正方形
∴AC⊥BD,OD=OC
∴∠DOG=∠COE=90°
∴∠OEC+∠OCE=90°
∵DF⊥CE
∴∠OEC+∠ODG=90°
∴∠ODG=∠OCE
∴△DOG≌△COE(ASA)
∴OE=OG
(2)①证明:∵OD=OC,∠DOG=∠COE=90°
又OE=OG
∴△DOG≌△COE(SAS)
∴∠ODG=∠OCE
②解:设CH=x,
∵四边形ABCD是正方形,AB=1
∴BH=1-x
∠DBC=∠BDC=∠ACB=45°
∵EH⊥BC
∴∠BEH=∠EBH=45°
∴EH=BH=1-x
∵∠ODG=∠OCE
∴∠BDC-∠ODG=∠ACB-∠OCE
∴∠HDC=∠ECH
∵EH⊥BC
∴∠EHC=∠HCD=90°
∴△CHE∽△DCH
∴![]()
∴HC2=EH·CD
得x2+x-1=0
解得![]() ,
,![]() (舍去)
(舍去)
∴HC=![]()

【题目】某蒜薹生产基地喜获丰收,收获蒜薹200吨.经市场调查,可采用批发、零售、冷库储藏后销售三种方式,并按这三种方式销售,计划平均每吨的售价及成本如下表:
销售方式 | 批发 | 零售 | 储藏后销售 |
售价(元/吨) | 3000 | 4500 | 5500 |
成本(元/吨) | 700 | 1000 | 1200 |
若经过一段时间,蒜薹按计划全部售出获得的总利润为y(元),蒜薹零售x(吨),且零售量是批发量的 ![]() .
.
(1)求y与x之间的函数关系式;
(2)由于受条件限制,经冷库储藏售出的蒜薹最多80吨,求该生产基地按计划全部售完蒜薹获得的最大利润.