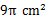题目内容
如图,BC是半圆的直径,AD BC,垂足为点D,弧BA=弧AF,BF与AD交于点E.
BC,垂足为点D,弧BA=弧AF,BF与AD交于点E.

(1)求证:AE=BE;
(2)若点A、F把半圆三等分,BC=12,求AE的长.
 BC,垂足为点D,弧BA=弧AF,BF与AD交于点E.
BC,垂足为点D,弧BA=弧AF,BF与AD交于点E.
(1)求证:AE=BE;
(2)若点A、F把半圆三等分,BC=12,求AE的长.
(1)证明见试题解析;(2) .
.
 .
.试题分析:(1)连AC,BC为直径,则∠BAC=90°,AD⊥BC,得∠C=∠BAE.由
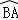 =
= ,可得∠C=∠ABF,所以∠ABE=∠BAE,从而证得AE=BE;
,可得∠C=∠ABF,所以∠ABE=∠BAE,从而证得AE=BE;(2)A,F把半圆三等分,则∠ACB=30°,由BC=12,得到AB=6,则AC=
 ,所以AD=
,所以AD= ,由∠BAD=30°,得到∠ABE=∠DBE=30°,故BD=3,DE=
,由∠BAD=30°,得到∠ABE=∠DBE=30°,故BD=3,DE= .
.解答:(1)证明:连AC,如图,∵BC为直径,则∠BAC=90°,∴∠C+∠ABC=90°,又∵AD⊥BC,∴∠BAE+∠ABC=90°,∴∠C=∠BAE,由
 =
=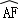 ,可得∠C=∠ABF,∴∠ABE=∠BAE,∴AE=BE;
,可得∠C=∠ABF,∴∠ABE=∠BAE,∴AE=BE;
(2)∵A,F把半圆三等分,∴∠ACB=30°,在直角三角形ABC中,BC=12,则AB=
 BC=6,AC=
BC=6,AC= AB=
AB= .在直角三角形ADC中,AD=
.在直角三角形ADC中,AD= AC=
AC= .∴AD=
.∴AD= ,∵∠C=∠ABF,∠ABE=∠BAE,∴∠ABE=∠BAE=30°,∠BED=30°,∴BD=3,ED=
,∵∠C=∠ABF,∠ABE=∠BAE,∴∠ABE=∠BAE=30°,∠BED=30°,∴BD=3,ED= ,∴AE=BE=
,∴AE=BE= .
.
练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
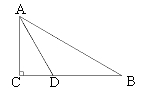
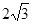 ,△ACD为等边三角形,CD、AB相交于点E.
,△ACD为等边三角形,CD、AB相交于点E.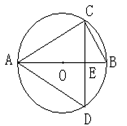
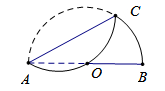
 ,∠AOC=( )
,∠AOC=( )

 cm
cm cm
cm cm或
cm或 cm
cm