题目内容
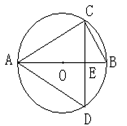
如图,在⊙O中,AB为⊙O的直径,C、D为⊙O上两点,弦AC=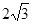 ,△ACD为等边三角形,CD、AB相交于点E.
,△ACD为等边三角形,CD、AB相交于点E.
(1)求∠BAC的度数;
(2)求⊙O的半径;
(3)求CE的长.
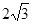 ,△ACD为等边三角形,CD、AB相交于点E.
,△ACD为等边三角形,CD、AB相交于点E.
(1)求∠BAC的度数;
(2)求⊙O的半径;
(3)求CE的长.
(1)30°;(2)2;(3) .
.
 .
.试题分析:(1)由直径所对圆周角为90°可以得到∠ACB=90°,再由圆周角定理得到∠D=∠B=60°,从而得到∠BAC的度数为30°;
(2)由∠BAC=30°,∠ACB=90°,用三角函数可以求出AB的长,进而求出半径的长;
(3)由△ACD为等边三角形,得到∠ACD=60°,又因为∠CAB=30°,所以∠AEC=90°,从而求出CE的长.
试题解析:(1)∵AB为⊙O的直径,∴∠ACB=90°,∵△ADC为等边三角形,∴∠ACD=∠D=60°,∵∠B=∠D,∴∠B=60°,∴∠BAC=30°;
(2)∵∠BAC=30°,∠ACB=90°,∴cos∠BAC=
 ,∴
,∴ ,解得:AB=4,∴⊙O的半径=2;
,解得:AB=4,∴⊙O的半径=2;(3)∵∠BAC=30°,∠ACD=60°,∴∠AEC=90°,∴CE=
 AC=
AC= .
.
练习册系列答案
相关题目
 BC,垂足为点D,弧BA=弧AF,BF与AD交于点E.
BC,垂足为点D,弧BA=弧AF,BF与AD交于点E.


 ,求弦MN的长.
,求弦MN的长.




