题目内容
【题目】在![]() 中,
中,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]()
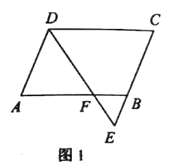
(1)如图1,若![]() ,则
,则![]() (直接写出结果) .
(直接写出结果) .
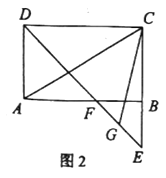
(2)如图2,若![]() 为
为![]() 的点,连接
的点,连接![]() ,求
,求![]() 的值;
的值;
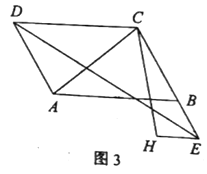
(3)如图3,若![]() 连接
连接![]() ,求
,求![]() 的值.
的值.
【答案】(1)3 (2)![]() (3)1
(3)1
【解析】
(1)由角平分线的定义和等腰三角形的判定与性质可得出AD=AF=2,BE=BF=1,则CD的长可求出;
(2)连接AG,BG,证明△AFG≌△CBG(SAS),可得AG=CG,∠AGF=∠CGB,则∠AGC=∠FGB=90°,可求出答案;
(3)分别延长DA,EH交于点N,连接CN,证明四边形DNEC是菱形,可得出△DCN和△CEN都是等边三角形,则CN=CE,∠DNC=∠NEC=60°,证明△ANC≌△HEC(SAS),得出AC=HC,则答案求出.
(1)如图
∵四边形ABCD为平行四边形,
∴DC∥AB,AD∥BC,
∴∠CDF=∠DFA,
∵∠ADC的平分线交AB于点F,
∴∠CDF=∠ADF,
∴∠ADF=∠DFA,
∴AD=AF=2,
∵AD∥BC,
∴∠E=∠ADF,
∵∠AFD=∠BFE,
∴∠BFE=∠E,
∴BE=BF=1.
∴AB=DC=2+1=3.
故答案为:3.
(2)如图,连接AG,BG.

∵四边形ABCD为平行四边形,∠ADC=90°,
∴四边形ABCD为矩形,
∴∠ABC=90°,
∴∠EBF=90°,
∵G为EF的中点,
∴FG=BG=EG,
∴∠BFG=∠FBG=45°,
∴∠AFG=∠CBG=135°,
∵∠AFD=∠BFG,
∴∠AFD=45°,
∴AD=AF,
∵AD=BC,
∴BC=AF,
∴△AFG≌△CBG(SAS),
∴AG=CG,∠AGF=∠CGB,
∴∠AGC=∠FGB=90°,
∴AC=![]() =
=![]() CG,
CG,
∴![]() ;
;
(3)如图,分别延长DA,EH交于点N,连接CN,

∵∠ADC=60°,DE平分∠ADC,
∴∠DCE=120°,∠CDE=30°,
∴∠CED=30°,
∴∠CDE=∠CED,
∴CD=CE,
∵EH∥AB,AB∥CD,
∴EN∥CD,
∵DN∥CE,
∴四边形DNEC为平行四边形,
∴四边形DNEC是菱形,
∴DC=DN,
∵∠ADC=60°,
∴△DCN和△CEN都是等边三角形,
∴CN=CE,∠DNC=∠NE=60°,
∵EH=BE,
∴AN=BE=EH,
∴△ANC≌△HEC(SAS),
∴AC=HC,
∴![]() =1.
=1.

【题目】某面包店推出一款新口味面包,每个成本1.5元,售价5元/个,试营业期间一律8折,每天只生产50个,为保持面包新鲜,当天未卖完的当天销毁,试营业期间市场日需求量(即每天所需数量)如表所示:
天数 | 8 | 10 | 10 | 2 |
日需求量/个 | 45 | 48 | 51 | 56 |
(1)补充日销售量(即每天销售的数量)的条形统计图;
(2)试营业期间某天的日需求量为45个,求当天的利润;
(3)求试营业期间(30)天的总利润

【题目】(10分)每年的6月5日为世界环保日,为提倡低碳环保,某公司决定购买10台节省能源的新机器,现有甲、乙两种型号的新机器可选,其中每台的价格、工作量如下表.
甲型机器 | 乙型机器 | |
价格(万元/台) | a | b |
产量(吨/月) | 240 | 180 |
经调查:购买一台甲型机器比购买一台乙型机器多2万元,购买2台甲型机器比购买3台乙型机器少6万元.
(1)求a、b的值;
(2)若该公司购买新机器的资金不能超过110万元,请问该公司有几种购买方案?
(3)在(2)的条件下,若公司要求每月的产量不低于2040吨,请你为该公司设计一种最省钱的购买方案.





