Question

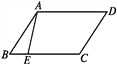
【题目】如图，，平分，平分，，相交于点，，．

（1）求证：四边形是菱形；

（2）若，，求的长．

Answer 1

【答案】（1）证明见解析；（2）．

【解析】

（1）利用，平分可得，从而得到，同理，由一组对边平行且相等可得四边形是平行四边形，再由一组邻边相等的平行四边形是菱形即可得证；

（2）由菱形的性质可知及其两直角边的长，根据勾股定理求得CD的长；由和可得四边形是平行四边形，再由得出四边形是矩形，根据矩形的对角线相等即可求得的长．

（1）证明：∵平分，

∴，

∵，

∴，

∴，

∴．

同理，

∴，，

∴四边形是平行四边形，

∴四边形ABCD是菱形；

（2）∵，，

∴四边形是平行四边形，

∵四边形是菱形，，，

∴，，，

∴，

在中，由勾股定理得，

∵四边形是平行四边形，，

∴四边形是矩形，

∴．