��Ŀ����
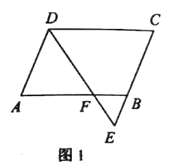
����Ŀ����ͼ1����![]() Ϊֱ��
Ϊֱ��![]() ��һ�㣬����
��һ�㣬����![]() ������
������![]() ��ʹ
��ʹ![]() ����һ��ֱ�����dzߵ�ֱ�Ƕ�����ڵ�
����һ��ֱ�����dzߵ�ֱ�Ƕ�����ڵ�![]() ����һ��
����һ��![]() ������
������![]() �ϣ���һ��
�ϣ���һ��![]() ��ֱ��
��ֱ��![]() ���·�������
���·�������![]() .
.

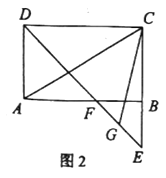
��1����ͼ1�е����dz��Ƶ�![]() ˳ʱ����ת��ͼ2��ʹһ��
˳ʱ����ת��ͼ2��ʹһ��![]() ��
��![]() ���ڲ�����ǡ��ƽ��
���ڲ�����ǡ��ƽ��![]() ����
����![]() �Ķ���;
�Ķ���;
��2����ͼ1�����dz��Ƶ�![]() ��ÿ��10���ٶ���˳ʱ�뷽����תһ�ܣ���ת�����У��ڵ� ��ʱ����
��ÿ��10���ٶ���˳ʱ�뷽����תһ�ܣ���ת�����У��ڵ� ��ʱ����![]() ǡ��������
ǡ��������![]() ƽ��;�ڵ� ��ʱ��ֱ��
ƽ��;�ڵ� ��ʱ��ֱ��![]() ǡ��ƽ�����
ǡ��ƽ�����![]() .
.
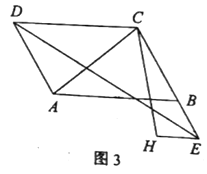
��3����ͼ1�е����dz��Ƶ�![]() ˳ʱ����ת��ͼ3��ʹ
˳ʱ����ת��ͼ3��ʹ![]() ��
��![]() ���ڲ�����̽��
���ڲ�����̽��![]() ��
��![]() ֮���������ϵ����˵������.
֮���������ϵ����˵������.
���𰸡�(1) 150��;(2) 9��27��6��24 ;(3)������.
��������
��1�����ݽ�ƽ���ߵĶ��������COM��Ȼ����ݡ�CON=��COM+90����𣻣�2���ֱ�������������ƽ���ߵ����ʺ���ת�����������ת�ǣ�Ȼ�������ת�ٶȼ��ɵý⣻
��3���á�BOM�͡�NOC��ʾ����BON��Ȼ���г������������ɵý⣮
�⣺��1����OMƽ�֡�AOC��
���COM=![]() ��AOC=60����
��AOC=60����
���CON=��COM+90��=150����
��2�����ߡ�AOC=120����
���BOC=60����
�ߡ�OMN=30����
�൱ON��ֱ��AB��ʱ��MN��OC��
��ת��Ϊ90����270����
��ÿ��˳ʱ����ת10����
��ʱ��Ϊ9��27��
ֱ��ONǡ��ƽ����ǡ�BOCʱ��
��ת��Ϊ60���� 180��+60��=240����
��ÿ��˳ʱ����ת10����
��ʱ��Ϊ6��24��
�ʴ�Ϊ��9��27��6��24��
��3���ߡ�MON=90������BOC=60����
���BON=90��-��BOM��
��BON=60��-��NOC��
��90��-��BOM=60��-��NOC��
���BOM-��NOC=30����
�ʡ�BOM���NOC֮���������ϵΪ����BOM-��NOC=30����